字节跳动面试题-水壶问题
问题
给你一个装满水的 8 升满壶和两个分别是 5 升、3 升的空壶,请想个优雅的办法,使得其中一个水壶恰好装 4 升水,每一步的操作只能是倒空或倒满。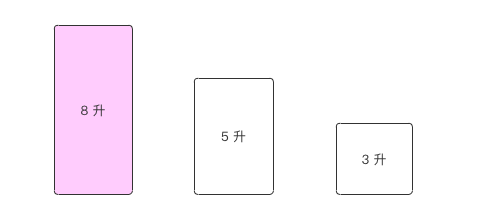
思路
先想想用人脑如何解决这个问题,模拟将水从一个水壶倒进另一个水壶,使得各个水壶水的体积不断变化,一步步尝试和推导,比如先正向推导,从已知状态推导后续状态,再反向推导,从结果状态往前推导,2种状态某一刻相同了,说明求出了答案,此方式较考验大脑的记忆能力和逻辑思维能力。
程序的方式和人脑相似,不过更为简单粗暴,俗称广度优先遍历剪枝算法,从初始状态开始,衍生出后续状态,每个后续状态只能是前一个状态下,从其中一个水壶倒向另一个水壶的一步操作,比如从(8,0,0)开始,只能倒水一次,则后续状态只能是(3,5,0)和(5,0,3),再从这2个状态继续向后衍生。所谓剪枝,是指后续状态不能再和前面任何一个状态重复。一直往后衍生,直到没有后续,或者找到了一种状态,表示正好有个水壶的水是4升。采用广度优先遍历,可保证我们的结果一定是最优解,也就是使用倒水的步骤一定是最少的。
从一个状态衍生后续状态的代码,倒水过程:
1 | |
广度优先遍历BFS算法:
1 | |
既然有了算法,不妨把这个变成此类问题的通用解。只需要得知3个参数:
1.所有容器的容量大小,此题为(8,5,3)
2.初始状态,此题为(8,0,0)
3.要得到的体积,此题为4
1 | |
结果
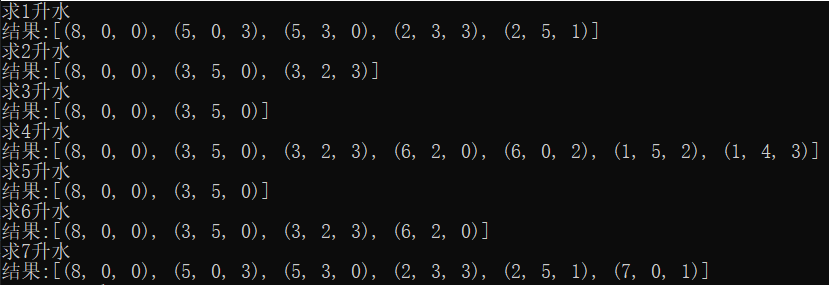
总结
数学VS计算机
| 数学 | 计算机 | |
|---|---|---|
| 解法 | 不定方程 | 暴力枚举 |
| 思想 | 人类智慧结晶 | 大量重复运算 |
个人觉得数学是人类文明几千年发展来的智慧结晶,而计算机只是人类历史上发明的一个重要工具。正是因为有了理论基础,才使工具的诞生有了可能,比如布尔代数的诞生,就大大简化了计算机逻辑电路的布线。
有了计算机这个工具,我们就可以在并不是那么“聪明”的情况下,也能解决具体问题。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 CodeTime!
评论