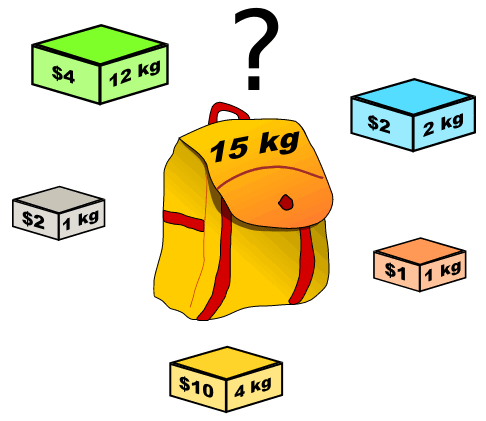植树节,我在腾讯种下了二百万棵树
腾讯极客技术挑战赛,码上种树,我种下了200万棵树。
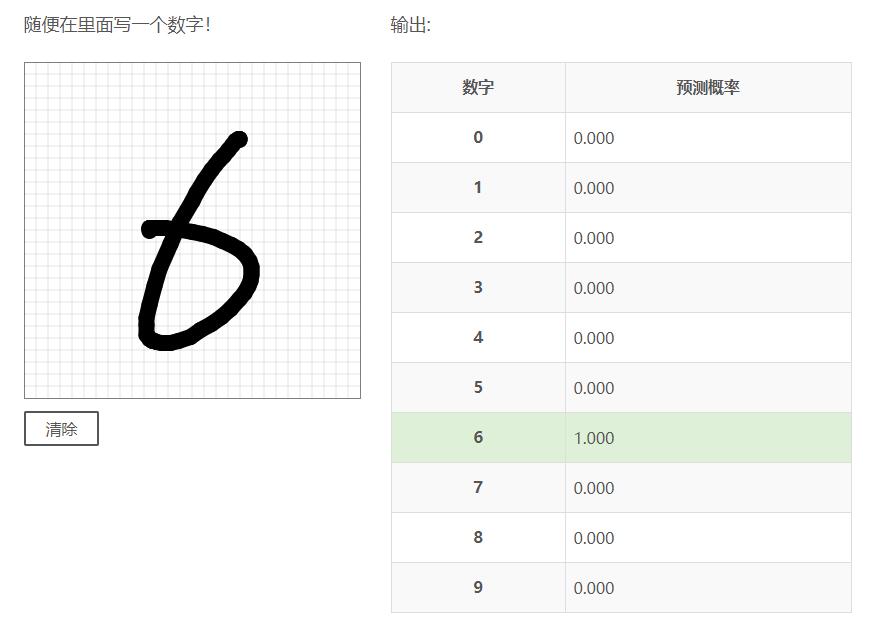
从手写数字识别开启人工智能的大门(附源码)
通过已知的输入和输出,来生成规则,程序通过大量样本数据的训练,使之越来越“明白”这个规则,从而能够预测未知输入的结果,这就是实现AI的其中一种方式。
一个模板搞定各种背包问题
前言背包问题实际上是动态规划的一种经典应用,本文想通过介绍一种模板用于解决各种背包问题。
模板统一采用二维数组来表示动态规划的状态,其中行表示物品的价值(或体积、大小、重量等),列表示背包的容量(或目标值)。
行和列都增加了一位,即从1开始计数,一来可以避免边界检查,二来dp[...][target]变得有意义,而非dp[...][target-1],具体值和数组索引能够对上。根据不同题意来初始化dp,需要注意的是只要涉及到取物品的值,我们需要对索引减1,因为我们是从1开始计数的。
接下来分三种情况考虑动态规划中的状态转移表达式:
完全背包(每件物品可以无限使用):dp[i][j]=OPERATE(dp[i-1][j],dp[i][j-objs[i-1]])。这里的OPERATE可以是sum、max、or视具体的问题而定。第二个表达式的索引是i。
1234567891011def bag_problem(self, bag: int, objs: List[int]) -> int: n=len(objs)+1 #将物品数量增加1,避免边界检查 #以下两行初 ...
为Spring Cloud Feign Client定制专属“装备”
详细介绍如何为 Spring Cloud 中的特定 FeignClient 实现配置隔离。
curl 参数用法详解
本文详细介绍了curl命令的常用参数和高级用法,包括发送请求、设置请求头、上传文件等功能,帮助读者掌握这一强大的命令行工具。
五分钟带你快速了解啥是“AIGC”
说起近期的热门科技词汇,AIGC当之无愧位列其中,但你真的了解AIGC吗?
从程序员的角度分析2024春晚刘谦魔术
原来刘谦不是会魔法,而是会算法。
深入理解Java并发包(JUC)中的锁与同步器
本文深入探讨了Java并发包(JUC)中的几种核心锁和同步器,通过原理讲解和代码示例,帮助开发者理解它们的使用场景和特性,提升并发编程能力。
读心术II
送给所有喜欢奥特曼的孩子们,这是为他们准备的魔术。
数据结构终极boss之红黑树
红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树,后在1978年被修改为如今的“红黑树”。因为它极其抽象,在数据结构中一直都宛如游戏boss一般的存在,希望通过该文章让你彻底理解红黑树的本质原理。