从程序员的角度分析2024春晚刘谦魔术

打乱

4张牌打乱从中间剪开并叠放得到8张牌，牌的顺序无关紧要，但剪开后的牌上下叠放，则2张相同的牌相互之间一定相隔4张，不妨假设这8张牌的排列顺序为ABCDABCD。

名字

无论名字有几个字，即将几张牌放到底部（最末端）得到的依然是个循环序列。比如名字2个字得到CDABCDAB，名字3个字得到DABCDABC。

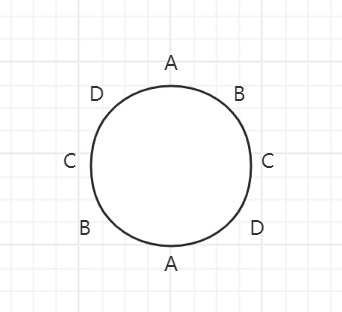
可以将这8张牌排成一个圆环，无论名字是几个字，也即无论从哪张牌作为圆环起点，始终都是在圆环中循环。

插入三张牌

观察即可发现，从这个环中任意位置取走连续的3张，则剩下的5张牌都会形成首尾相同的一个序列：

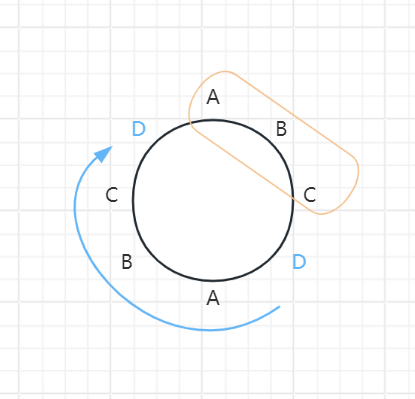
将取走的3张牌插入到序列的中间位置（注意不能插到最底部），则一定能得到一个由8张牌构成的并且首尾相同的序列AxxxxxxA。

隐藏第一张牌

根据规则，将第1张牌隐藏起来，后续经过一系列摆放和丢弃操作，最终目的都是为了将最末尾的牌留下来，而这张牌正好和隐藏的牌相同，可拼在一起，实现了魔术效果。

由于最后结果只和序列最后一张牌有关，其他牌都需要丢弃，此时序列为长度为7的xxxxxxA，x表示其他牌，A表示隐藏牌。

南北方

取出序列开头任意的1张2张或3张牌并插入中间，此时并没有改变序列最末尾的牌，而序列中其他牌的位置是对结果没有任何影响的，所以该操作可有可无，刘谦可能只是为了增加神秘感或者让观众更有参与感才加入该步骤。尼格买提可能正是在该步骤将牌插入了末尾，改变了序列中最末尾的牌才导致结果错误。此时序列仍然可看作是xxxxxxA。

性别

男生丢弃最开头1张牌，形成长度为6的序列xxxxxA；女生丢弃最开头的2张牌，形成长度为5的序列xxxxA。

咒语

“见证奇迹的时刻”共7个字，则需要将序列最开头的牌移到最末尾共执行7次。男生的牌有6张，6次为一个闭环（6次后序列相当于未发生任何改变），则相当于执行7-6=1次；同理，女生的牌有5张，则5次为一个闭环，相对于执行7-5=2次。男女生的最终序列分别为xxxxAx和xxAxx。

好运留下来，烦恼丢出去

将序列第1张牌插入末尾，并丢弃第2张，将第3张牌插入末尾，并丢弃第4张，以此类推，直到剩下最后一张。这很容易让人想到一个通用问题，假如有n张牌排成一个圆环，并且从1到n按顺序排列，如果一直按上述规则操作，那么最后剩下那张牌的编号是几呢？

其实这个问题早就有人研究过了，它还有一个经典名字叫做约瑟夫环。答案就是，如果这个n恰好可以表示为2的多少次方，比如16正好是2的4次方，8正好是2的3次方，那么最终留下牌的一定是编号1。

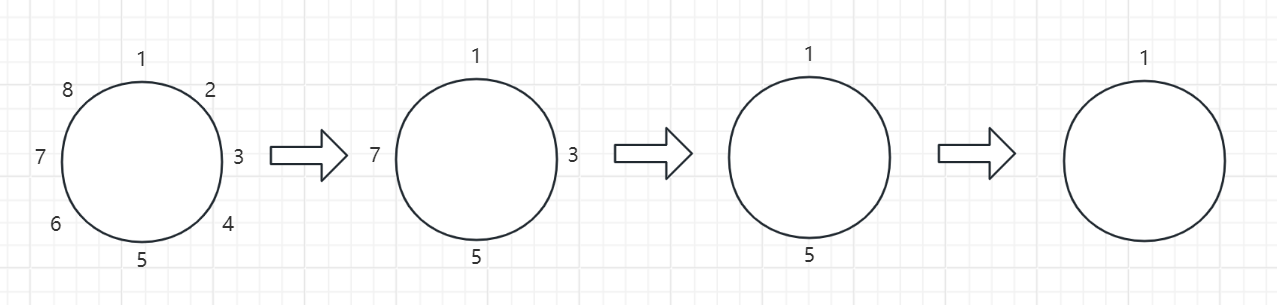
观察可发现，如果n正好是2的x次幂（$ n=2^x $），那么第一轮会正好丢弃掉 $ 2^{x-1} $张牌，同时第二轮依然会从编号1开始计数，然后丢弃掉 $ 2^{x-2} $ 张牌……，每一轮都会从编号1开始，直到最后丢弃 $ 2^0=1 $ 张牌只剩下编号1。

换个角度，如果一个数n正好是2的整数次方，那么这个数用二进制表示，它的数位中只会有一个1，比如16的二进制为1000，8的二进制位100，它们都只有最高位的一个1。

对于任意数n来说，我们都可以表示为 $ n=2^x+a $ 。我们可以考虑先丢弃掉a张牌，则剩下的 $ 2^x $ 张牌中，第1张牌一定是最终留下的那张，因为如果对剩下的牌重新从1开始编号，这张牌就是编号1。对于要丢弃掉a张牌，由于是留1去1，则需要数到编号2a，才能正好丢弃a张，所以编号2a+1则是剩下 $ 2^x $ 张牌中的第1张。

比如对于n=7，$ 7=2^2+3 $，a=3，丢弃3张牌好正好剩下 $ 2^2=4 $ 张牌，则走到编号6时正好剩下4张牌，而对于这剩下的4张牌重新编号，则编号7成为了编号1。所以n=7时，答案为7，也就是 $ 2a+1=2*3+1=7 $。

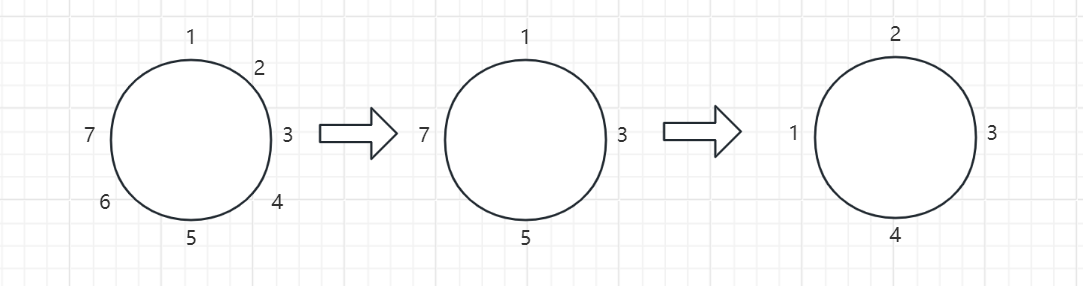
也就是说对于任意数n，$ n=2^x+a $，只要算出a，那么就能计算出答案，为2a+1。

站在程序员的角度，a的值等于n去除二进制表示中最高位后的值，用代码实现约瑟夫环的这个问题为：

def JosephRing(n):
    for i in range(32):  # 假设n最大不超过32位
        j = 1 << (31 - i)
        if n & j:
            n = n ^ j    # 移除最高位的1
            break
    return n * 2 + 1