前言

之前在讨论二叉搜索树的时候，已经介绍过一种可高度平衡的二叉搜索树，即AVL平衡二叉树。现在我们将介绍另一种鼎鼎有名的平衡二叉树-红黑树，它因节点存储红或黑两种颜色之一而命名。相较于AVL树，它是一种弱平衡二叉树，不需要像AVL树那样严格要求平衡，这也导致它的查询效率并没有AVL树那么高，但相对的，它带来的好处是对于调整失衡，红黑树的旋转次数更少，所以频繁的插入或删除操作，红黑树更有优势。

定义

引用自百度百科：

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。

红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。

由于每一棵红黑树都是一颗二叉排序树，因此，在对红黑树进行查找时，可以采用运用于普通二叉排序树上的查找算法，在查找过程中不需要颜色信息。

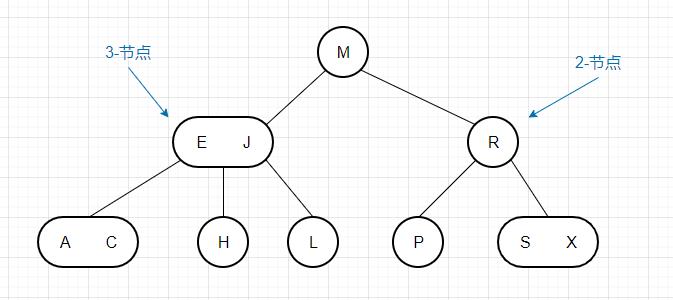
2-3搜索树

在介绍红黑树之前，我们需要先了解一下什么是2-3搜索树。顾名思义，2-3搜索树也是一种搜索树，不过相较于一般的二叉搜索树，它的节点不仅可以存储1个键，还可以存储2个键，也就是说，它包含2种类型的节点：

  • 2-节点：含有一个键和两条链接，左链接指向的节点的键都小于该节点的键，右链接指向的节点的键都大于该节点的键。这也就是传统二叉搜索树的节点。
  • 3-节点：含有两个键和三条链接，左链接指向的节点的键都小于该节点的小键，右链接指向的节点的键都大于该节点的大键，中链接指向的节点的键都介于该节点两个键之间。

简单起见，我们这里提到的2-3查找树都是指完美平衡的2-3查找树，完美平衡表示树中所有的叶子节点到根节点的距离都是相同的。我们之后将介绍如何维持这种平衡，以下是一棵2-3查找树的例子：

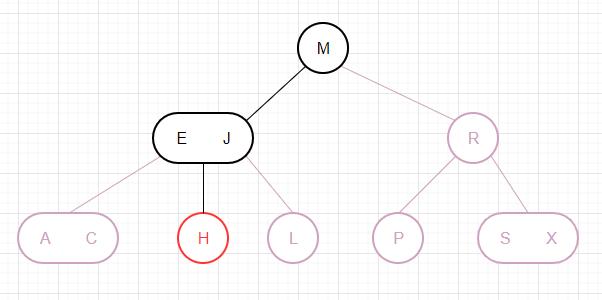
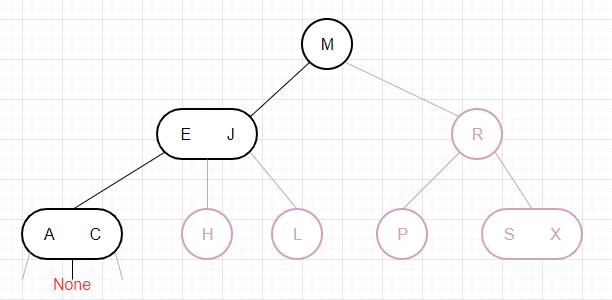
查找

要判断一个键是否在树中，我们先将它和根结点中的键比较。如果它和其中任意一个相等，查找命中；否则我们就根据比较的结果找到指向相应区间的链接，并在其指向的子树中递归地继续查找。如果这是个空链接，查找未命中。

以下是2个例子，对于H的命中查找：

命中查找

对于B的未命中查找：

未命中查找

插入

要在 2-3 树中插入一个新节点，我们可以和二叉查找树一样先进行一次未命中的查找，然后把新节点挂在树的底部。但这样的话就破坏了树的完美平衡性，我们需要继续维持这种平衡性。以下根据2种插入情况分别讨论。

插入在2-节点

如果未命中的查找结束于一个2-节点，事情就好办了，我们只要把这个2-节点替换为一个3-结点，将要插入的键保存在其中即可，比如在树中插入K：

  • 对K的查找在2-节点结束

  • 将2-节点替换为3-节点

插入在3-节点

如果未命中的查找结束于一个3-结点，则相对麻烦一些。我们会得到一个临时的4-节点，而4-节点在2-3树中并不被允许，我们需要将它进行分解。分解步骤为将4-节点分解为3个2-节点，然后将中键插入到它的父节点中。如果父节点是2-节点则转变为3-节点，然后停止；如果父节点是3-节点，则变成临时的4-节点，然后继续分解并向上转移，直至最终转移到根节点。根节点分解后，会使树的高度增加1，但仍然维持了树的完美平衡性。比如在树中插入Z：

  • 对Z的查找在3-节点结束

  • 将3-节点替换为临时的4-节点

  • 4-节点分解为3个2-节点，中间节点上移至父节点

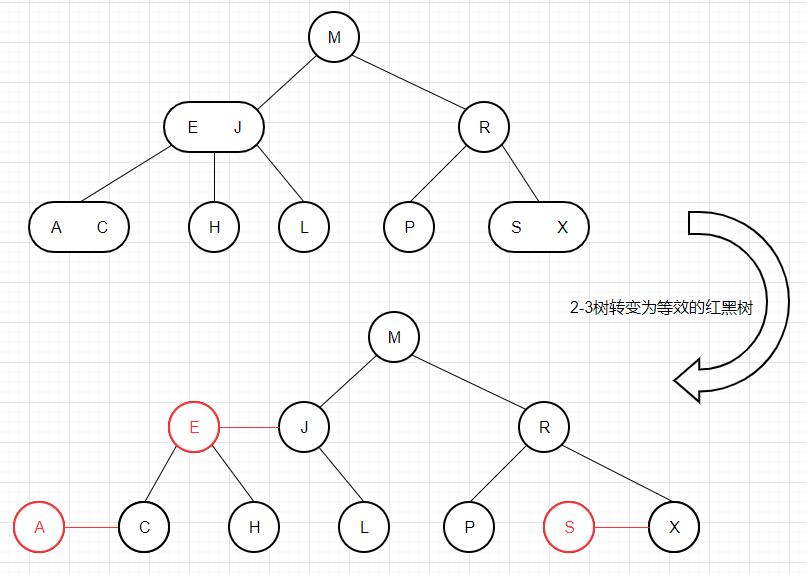
红黑树

理解了2-3树的原理，接下来，我们定义一种名为红黑树的数据结构，它使用标准的二叉搜索树（完全由2-节点构成的树）以及一些额外的信息（颜色，用于替换3-节点）来模拟2-3树的实现。

我们将树中的链接分为两种类型：

  • 红链接：将两个2-节点连接起来构成一个3-节点；
  • 黑链接：2-3树中的普通链接；

准确的说，我们将3-节点表示为一条左斜的红色链接相连的两个2-节点。根据我们的定义，这棵红黑树应该是一棵满足如下条件的二叉搜索树：

  1. 红链接均为左链接；
  2. 没有任何一个节点同时和两条红链接相连；
  3. 该树是完美黑色平衡的，即任意空链接到根节点的路径上的黑链接数量相同。

如果将这棵红黑树的所有红链接画平，并将由红链接相连的节点看成一个整体，那么我们会发现，它和2-3树是一模一样的。

颜色表示

除了根节点外，每个节点都只会有一条指向自己的链接（由它的父节点指向它），我们将链接的颜色保存在节点中，同时我们规定指向空节点和根节点的链接颜色为黑色。我们定义如下的数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
const bool RED = true;
const bool BLACK = false;
class Node
{
    public TKey key;
    public Node left, right;
    public bool color;
    public Node(TKey key)
    {
        this.key = key;
        color = RED;
    }
}

我们再封装一个私有方法，以确保可以获得任意节点（包含空节点）和它父节点的链接颜色：

1
2
3
4
5
6
private bool isRed(Node x)
{
    if (x == null)
        return false;
    return x.color == RED;
}

旋转

与AVL树类似，我们在执行完某些操作后，可能会出现红色右链接或者两条连续的红色左链接，这破坏了我们之前关于红黑树的约定，需要对其进行修复，其中最基本的操作就是旋转。

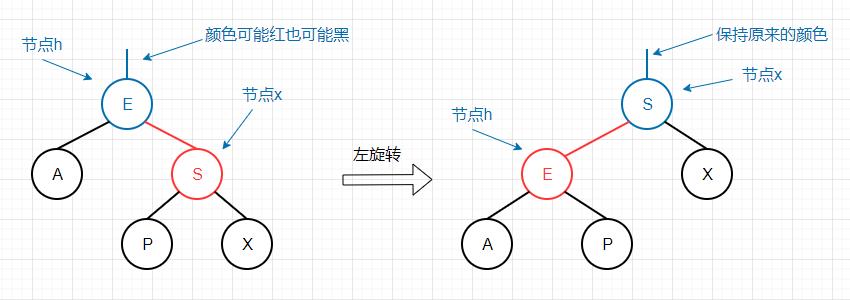
左旋转

其实现目标为将红色右链接转换为红色左链接。

1
2
3
4
5
6
7
8
9
private Node rotateLeft(Node h)
{
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = RED;
    return x;
}

旋转之后，我们返回x作为新的根节点，同时x保留了原来根节点h的颜色。

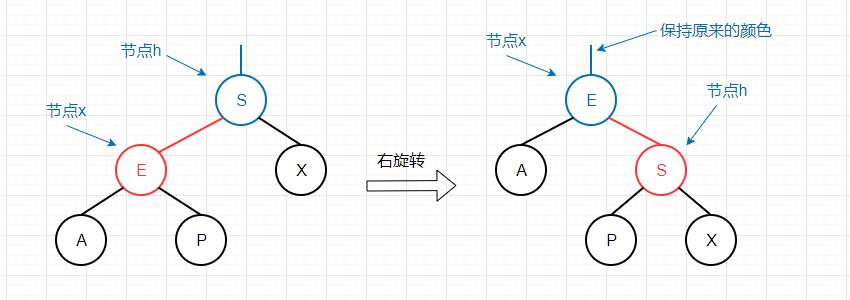
右旋转

其实现目标为将红色左链接转换为红色右链接，该旋转目的主要是为了消除连续的红色左链接。

1
2
3
4
5
6
7
8
9
private Node rotateRight(Node h)
{
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    return x;
}

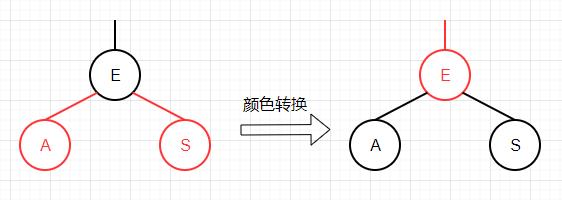
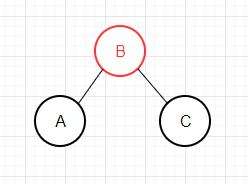
颜色转换

我们通过旋转会消除红色右链接或者两条连续的红色左链接的情况，但最终可能会出现一种情况，亦即某个节点同时拥有左右2个红色子节点。

我们定义一个flipColors方法来转换一个节点的两个红色子节点的颜色。除了将子结点的颜色由红变黑之外，同时还将父结点的颜色由黑变红。这项操作最重要的性质在于它和旋转操作一样是局部变换，不会影响整棵树的黑色平衡性。

1
2
3
4
5
private void flipColors(Node h)
{
    h.color = RED;
    h.left.color = h.right.color = BLACK;
}

这个操作相当于在2-3树中，我们将临时的4-节点分解为3个2-节点，同时让中间节点和父节点相结合，并一直向上转移。

注意：根节点始终是黑色，因为红色的根节点表示根节点是一个3-节点的一部分，这并不符合实际情况。所以如果我们对根节点进行了flipColors操作，需要将根节点设置为黑色（实际操作中，每次调整失衡我们都将根节点设置为了黑色）。对根节点进行flipColors操作，同时也意味着树的黑链接高度增加了1。

插入操作

我们使用二叉搜索树相同的方式往红黑树中插入节点，插入会发生在树的叶子节点上，可能是2-节点也可能是3-节点。我们统一使用红链接将新节点和它的父节点相连。

在2-节点中插入新键

  1. 新键小于2-节点的键

    此情况无须做任何操作，插入完成后本身就是一个合法的3-节点。

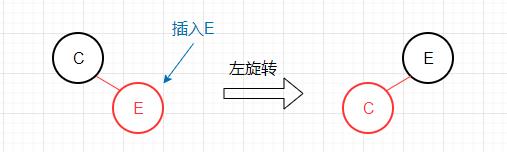
  2. 新键大于2-节点的键

    此情况需进行一次左旋转，将红色右链接转变成左链接，变成一个合法的3-节点。

在3-节点中插入新键

  1. 新键大于3-节点的最大键

    此情况无须任何旋转操作。

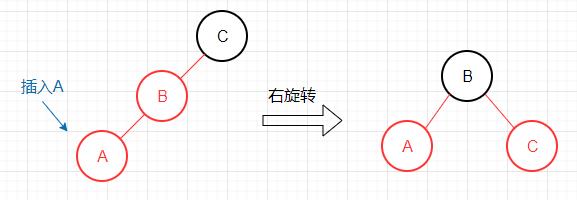
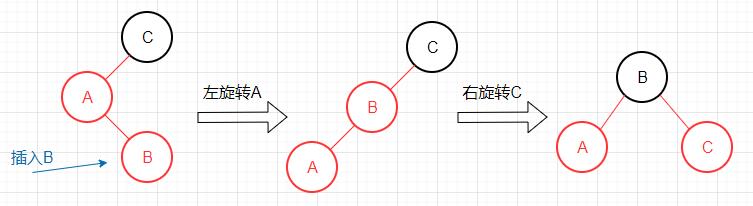
  2. 新键小于3-节点的最小键

    此情况出现了两条连续的红色左链接，需对节点C做右旋转。

  3. 新键介于3-节点两个键之间

    此情况出现了红色左链接以及两条连续的红色左链接，需进行两次旋转。

此三种情况最终都会产生一个同时连接到两条红链接的节点，此时我们进行一次颜色转换操作即可完成修复。

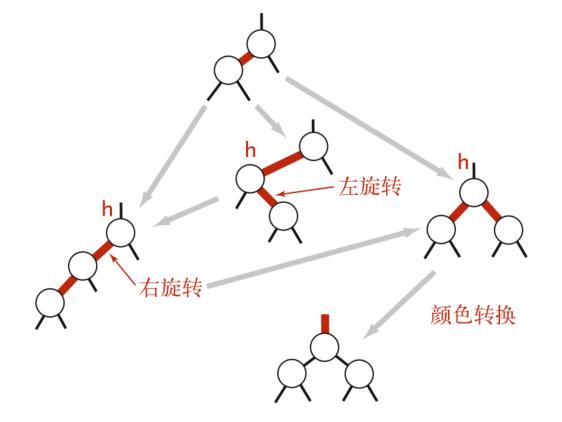
调整失衡

针对以上情况总结，我们可以得到如下规律：

  • 如果右子节点是红色的而左子节点是黑色，进行左旋转；
  • 如果左子节点是红色的且它的左子节点也是红色的，进行右旋转；
  • 如果左右子节点均为红色，进行颜色转换。

对于某个节点调整失衡的实现代码：

1
2
3
4
5
6
7
8
9
10
11
private Node balance(Node h)
{
    if (isRed(h.right) && !isRed(h.left))
        h = rotateLeft(h);
    if (isRed(h.left) && isRed(h.left.left))
        h = rotateRight(h);
    if (isRed(h.left) && isRed(h.right))
        flipColors(h);
    h.N = size(h.left) + size(h.right) + 1;
    return h;
}

最终我们实现的插入操作和普通二叉搜索树几乎一模一样，只是插入完成后，需要由叶子节点至底向上，一步步为查找路径上的节点调整平衡。

1
2
3
4
5
6
7
8
9
10
11
private Node put(Node h, TKey key)
{
    if (h == null)
        return new Node(key);
    int cmp = compare(key, h.key);
    if (cmp < 0)
        h.left = put(h.left, key);
    else if (cmp > 0)
        h.right = put(h.right, key);
    return balance(h);
}

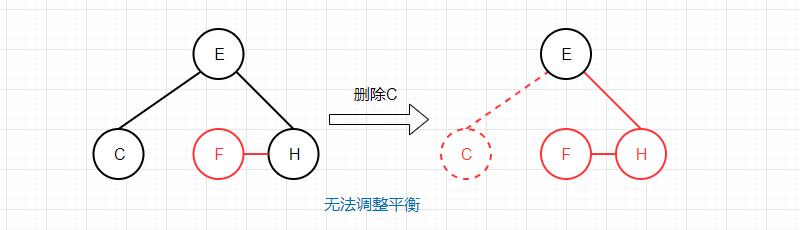
删除操作

红黑树的删除操作较为复杂和难以理解，不过我们这里仍然以2-3树为例，首先明确在2-3树中应该如何操作后仍然保持平衡，再使用我们定义的红黑树来模拟这个过程。简单起见，我们先从删除最小键开始。

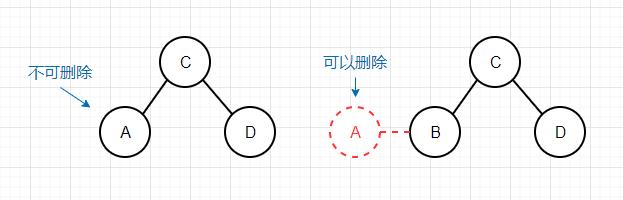
删除最小键

在二叉搜索树中，最小键就是树最左边的节点，所以如果某个节点的左节点为空，那么这个节点就是最小节点，在一般二叉搜索树中，我们只需要将这个节点的右节点赋值给它的父节点，即完成了最小节点的删除。但是在2-3树中，我们不能将节点留空，因为这样就失去了平衡。可以考虑这样一种情况，假如我们要删除的最小键是在一个3-节点中，这样一来当我们删除这个键的时候，3-节点就变成了2-节点，对于2-3树来说就依然是平衡的。

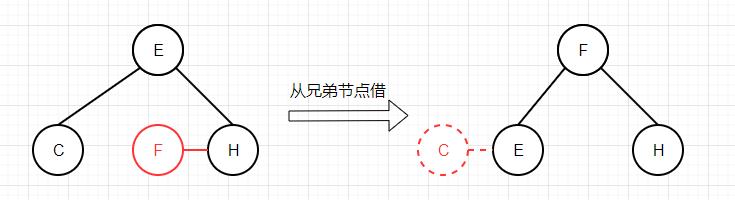
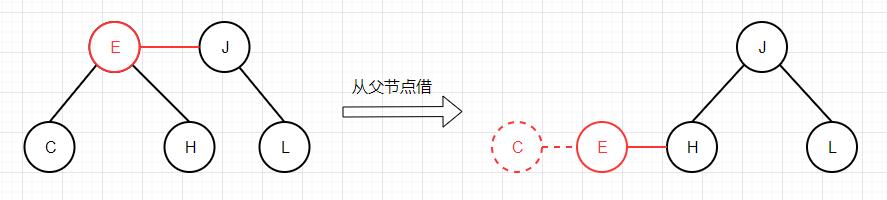
接下来，我们定义一个共用方法moveRedLeft，该方法进行一系列转换，确保最小键一定位于最底端的3-节点（或4-节点）中，以下是moveRedLeft方法进行的2种转换：

  • 从兄弟节点借变成3-节点后删除

  • 从父节点借变成4-节点后删除

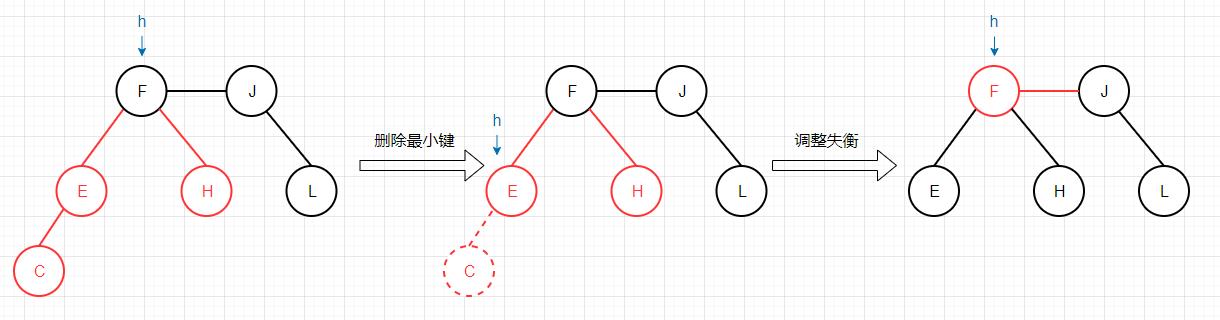
对于deleteMin方法，我们自顶向下递归，当我们找到最小节点（最左边的节点）时，直接返回空即可，否则继续对子节点进行变换。该变换可能导致会出现4-节点，不过不用担心，因为最后我们会通过之前的调整失衡balance方法自底向上来消除这种情况。 

1
2
3
4
5
6
7
8
private Node deleteMin(Node h)
{
    if (h.left == null)
        return null;
    h = moveRedLeft(h);
    h.left = deleteMin(h.left);
    return balance(h);
}

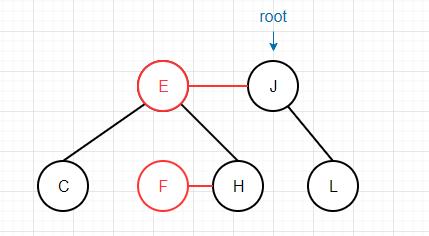
最后，我们以下面这棵红黑树为例，来理解moveRedLeft方法的实现

首先如果节点本身是3-节点，或者其左子节点是3-节点时，则无需任何处理，直接递归其左子节点即可，比如对该树根节点进行moveRedLeft操作会直接返回。

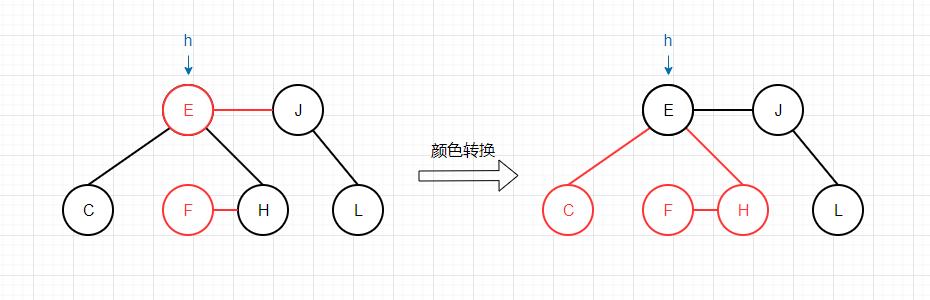
否则我们进行颜色变换，将父节点融合进来，变成4-节点：

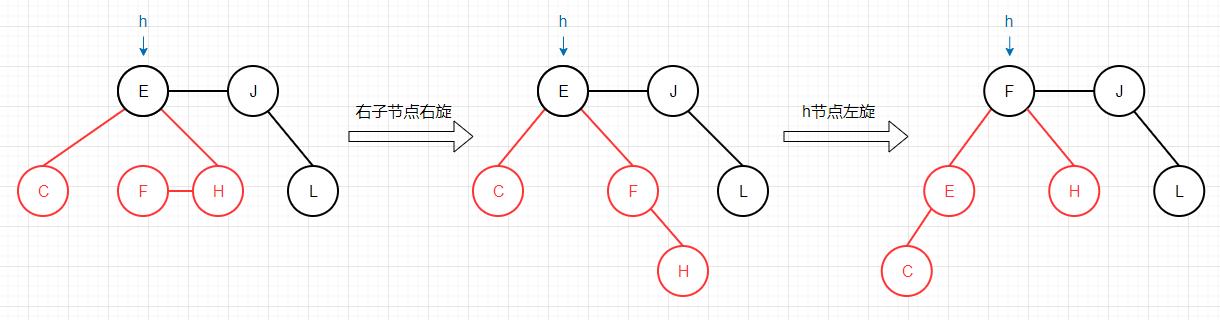
如果节点的右子节点为2-节点，则还需要对其进行旋转操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private Node moveRedLeft(Node h)
{
    //当节点本身是2-节点，或者其左子节点是3-节点时，无需处理
    if (isRed(h.left) || isRed(h.left.left))
        return h;
    //颜色转换，相当于从父节点借
    h.color = BLACK;
    h.left.color = h.right.color = RED;
    //旋转，相当于从兄弟节点借
    if (isRed(h.right.left))
    {
        h.right = rotateRight(h.right);  //右子节点右旋
        h = rotateLeft(h);               //h节点左旋
    }
    return h;
}

处理完毕之后，我们便可毫无顾虑的删除最小键，最后再通过平衡操作，调整成一棵合法的红黑树。

注意到这里的转换颜色操作和之前介绍的flipColors方法恰好相反，我们可以将该方法抽离出来：如果是自底向上进行调整失衡，我们定义参数top为true；如果是自顶向下，融合父节点操作，则定义参数top为false。

1
2
3
4
5
6
7
8
9
10
11
12
13
private void flipColors(Node h, bool top)
{
    if (top)
    {
        h.color = RED;
        h.left.color = h.right.color = BLACK;
    }
    else
    {
        h.color = BLACK;
        h.left.color = h.right.color = RED;
    }
}

类似于插入叶子节点，当最终删除最小键后，也需要自底向上平衡到根节点，此时我们需要将根节点置为黑色。

1
2
3
4
5
6
7
8
public void deleteMin()
{
    if (root == null)
        return;
    root = deleteMin(root);
    if (root != null)
        root.color = BLACK;
}

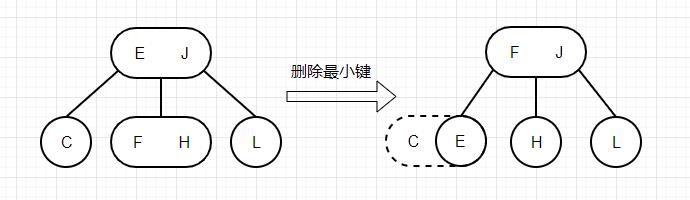
通过以上的例子，可以观察到对于红黑树最小键的删除过程，实际体现在2-3树中的结果如下图所示：

删除任意键

现在我们考虑在红黑树中删除任意键的算法，在删除最小键的时候我们通过变换让最小键位于3-或4-节点中再进行删除，其中用到了moveRedLeft方法，该方法保证让右边的节点3-节点可以转移到左边到2-节点，现在当我们要删除的键可能位于右边的2-节点时，也需要考虑将左边的3-节点转移到右边的2-节点中，类似地，我们定义moveRedRight方法：

1
2
3
4
5
6
7
private Node moveRedRight(Node h)
{
    if (isRed(h.right) || isRed(h.right.left))
        return h;
    flipColors(h, false);
    return h;
}

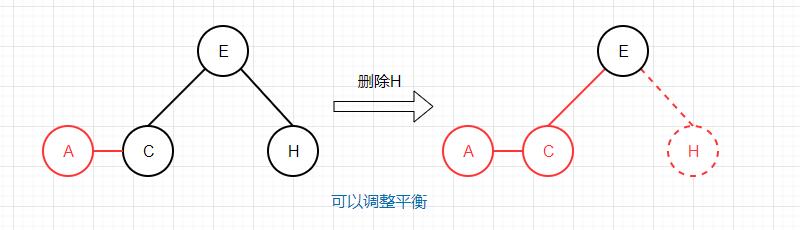
相比较moveRedLeft而言，这里除了颜色转换没用到任何旋转，因为我们约定红连接都是左链接，根据我们的平衡算法，即使没有从左兄弟节点转移到右2-节点，最后调整平衡的时候也可以恢复正常的，比如删除一个2-节点H：

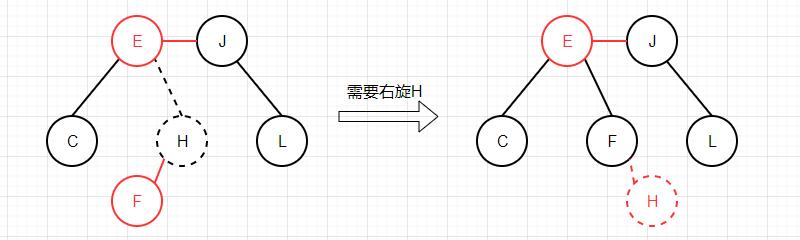
而如果要删除的键在左边的2-节点中，则无法直接恢复平衡，删之前需先旋转：

值得注意的是，因为红链接都是在左侧，所以一个3-节点中较大的那个键为父节点，假如要删除的是这个大键，那么必须先进行右旋转，让小键提升为父节点再进行删除，而如果要删除的是小键就没有必要了，因为它本身就是一个左子节点。

比如这里如果删除的键是H则需要右旋转，而如果是F则无需旋转：

最后，我们来剖析一下完整的删除算法，首先从根节点开始和删除键进行比较：

  • 小于当前键，递归左子节点，类似于删除最小键的做法，递归前需先执行融合方法moveRedLeft：
    • 没有左子节点：已经不存在更小的键了，抛出异常；
    • 有左子节点：继续递归左子节点；
  • 大于等于当前键，先判断是否需要进行右旋转（把大键旋转到右侧），然后分情况：
    • 没有右子节点：
      • 等于当前键：直接返回空；
      • 大于当前键：已经不存在更大的键了，抛出异常；
    • 有右子节点，先通过moveRedRight方法融合：
      • 等于当前键：将当前节点的键替换成右子树的最小键，同时删除右子树的最小键；
      • 大于当前键：继续递归右子节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
private Node delete(Node h, TKey key)
{
    if (h == null)
        throw new KeyNotFoundException("给定关键字不在字典中。");
    if (compare(key, h.key) < 0)
    {
        if (h.left == null)
            throw new KeyNotFoundException("给定关键字不在字典中。");
        h = moveRedLeft(h);
        h.left = delete(h.left, key);
    }
    else
    {
        if (isRed(h.left))
            h = rotateRight(h);
        if (h.right == null)
        {
            if (compare(key, h.key) == 0)
                return null;
            throw new KeyNotFoundException("给定关键字不在字典中。");
        }
        h = moveRedRight(h);
        if (compare(key, h.key) == 0)
        {
            var m = min(h.right);
            h.key = m.key;
            h.right = deleteMin(h.right);
        }
        else
            h.right = delete(h.right, key);
    }
    return balance(h);
}

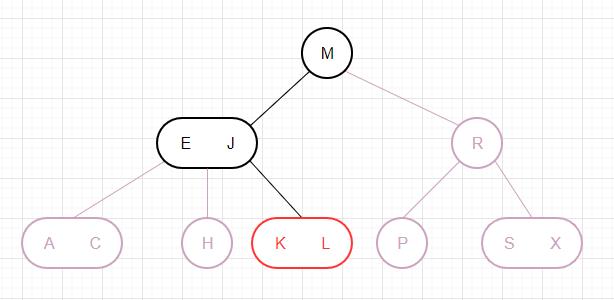
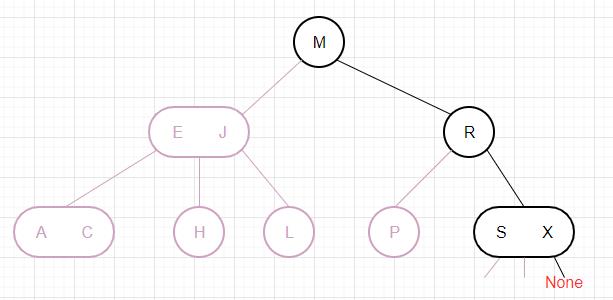
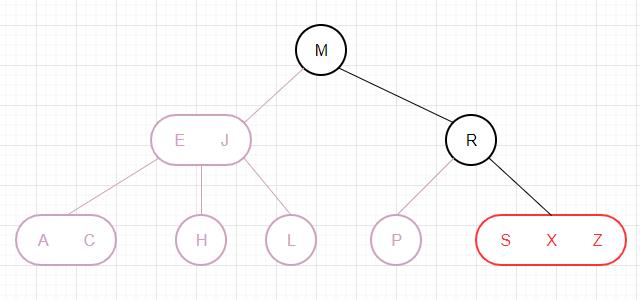
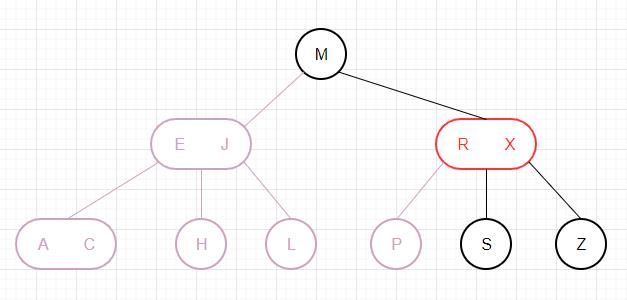
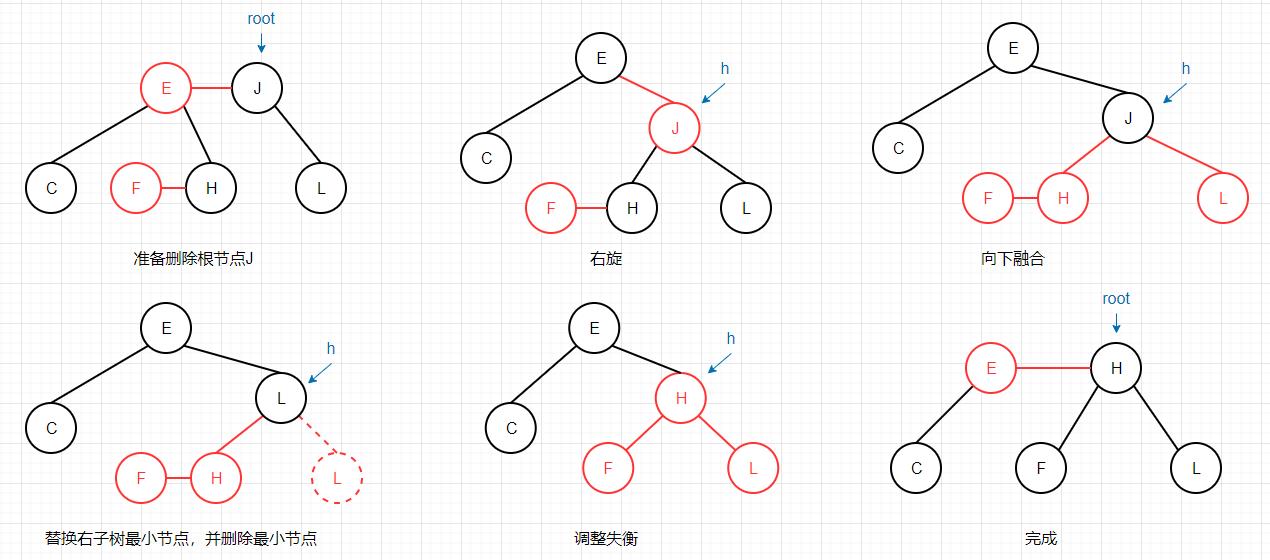
下面我们以删除一棵红黑树的根节点为例，通过图片来演示算法是如何运作的：

完整代码

如果忽略这棵红黑树的颜色属性，那么它就是一棵普通的二叉搜索树，只不过它是高度平衡的，所以查询相关的代码和普通二叉搜索树完全一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
public class RedBlackBST<TKey>
{
    const bool RED = true;
    const bool BLACK = false;
    class Node
    {
        public TKey key;
        public Node left, right;
        public bool color;
        public Node(TKey key)
        {
            this.key = key;
            color = RED;
        }
    }

    public RedBlackBST(IComparer<TKey> comparer)
    {
        compare = comparer.Compare;
    }

    private Node root;
    private Func<TKey, TKey, int> compare;

    private bool isRed(Node x)
    {
        if (x == null)
            return false;
        return x.color == RED;
    }

    private Node rotateLeft(Node h)
    {
        Node x = h.right;
        h.right = x.left;
        x.left = h;
        x.color = h.color;
        h.color = RED;
        return x;
    }

    private Node rotateRight(Node h)
    {
        Node x = h.left;
        h.left = x.right;
        x.right = h;
        x.color = h.color;
        h.color = RED;
        return x;
    }

    private void flipColors(Node h, bool top)
    {
        if (top)
        {
            h.color = RED;
            h.left.color = h.right.color = BLACK;
        }
        else
        {
            h.color = BLACK;
            h.left.color = h.right.color = RED;
        }
    }
    
    private Node balance(Node h)
    {
        if (isRed(h.right) && !isRed(h.left))
            h = rotateLeft(h);
        if (isRed(h.left) && isRed(h.left.left))
            h = rotateRight(h);
        if (isRed(h.left) && isRed(h.right))
            flipColors(h, true);
        return h;
    }
    
    public void put(TKey key)
    {
        root = put(root, key);
        root.color = BLACK;
    }
    
    private Node put(Node h, TKey key)
    {
        if (h == null)
            return new Node(key);
        int cmp = compare(key, h.key);
        if (cmp < 0)
            h.left = put(h.left, key);
        else if (cmp > 0)
            h.right = put(h.right, key);
        return balance(h);
    }
    
    private Node moveRedLeft(Node h)
    {
        if (isRed(h.left) || isRed(h.left.left))
            return h;
        flipColors(h, false);
        if (isRed(h.right.left))
        {
            h.right = rotateRight(h.right);
            h = rotateLeft(h);
        }
        return h;
    }

    private Node moveRedRight(Node h)
    {
        if (isRed(h.right) || isRed(h.right.left))
            return h;
        flipColors(h, false);
        return h;
    }

    public void deleteMin()
    {
        if (root == null)
            return;
        root = deleteMin(root);
        if (root != null)
            root.color = BLACK;
    }
    
    private Node deleteMin(Node h)
    {
        if (h.left == null)
            return null;
        h = moveRedLeft(h);
        h.left = deleteMin(h.left);
        return balance(h);
    }

    public void delete(TKey key)
    {
        root = delete(root, key);
        if (root != null)
            root.color = BLACK;
    }
    
    private Node delete(Node h, TKey key)
    {
        if (h == null)
            throw new KeyNotFoundException("给定关键字不在字典中。");
        if (compare(key, h.key) < 0)
        {
            if (h.left == null)
                throw new KeyNotFoundException("给定关键字不在字典中。");
            h = moveRedLeft(h);
            h.left = delete(h.left, key);
        }
        else
        {
            if (isRed(h.left))
                h = rotateRight(h);
            if (h.right == null)
            {
                if (compare(key, h.key) == 0)
                    return null;
                throw new KeyNotFoundException("给定关键字不在字典中。");
            }
            h = moveRedRight(h);
            if (compare(key, h.key) == 0)
            {
                var m = min(h.right);
                h.key = m.key;
                h.right = deleteMin(h.right);
            }
            else
                h.right = delete(h.right, key);
        }
        return balance(h);
    }      
    
    private Node min(Node x)
    {
        if (x.left == null)
            return x;
        return min(x.left);
    }
}

参考文献：《算法》第四版