Google经典面试题-扔鸡蛋

这是一道Google公司的经典面试题，有多经典呢？经典到Google公司已经不用它做面试了！

问题

假设有一栋大楼有100层，其中有1层比如F层，你从这一层或者比它低的层往下扔鸡蛋，鸡蛋不会碎，但是从比F层高的楼层开始扔，鸡蛋一定会碎。也就是说F层是个临界点，你的任务就是找到F层，同时给你2个鸡蛋，你能最少实验多少次（或者说扔多少次鸡蛋）能找到这个F层。

解答

这个问题不是简单的二分查找问题，假如给你无数个鸡蛋，确实可以采用二分查找的方式，比如先从50层开始扔，如果碎了说明F层在50层之下，然后再从25层继续。。。如果没碎，说明在50层以上，下一个从75层开始扔。根据$ \log_2 100 \approx 6.64 $，说明只要7次一定能找到这个F。
但是现在只有2个鸡蛋，假如第一个鸡蛋在50层就碎了，那么你只能知道F在1到50之间，但是只剩下一个鸡蛋了，你只能从1楼开始一层一层往上试，因为你不能让蛋碎掉，一旦碎了就无法后续测试了。假如F正好是49，也就是说你一直试到49都没有碎，那么你总共扔了50次蛋才得到结果。
有没有办法可以实验最少次，一定能找到结果。答案是有的，比如这题的答案就是14，它采取的策略是：

第1个蛋分别从楼层14、27、39、50、60、69、77、84、90、95、99、100开始试，假如在14层碎了，第2个蛋就实验1-13层，最坏情况13+1=14次；假如14层没碎，在27层碎了，第2个蛋就实验15-26层，最坏情况是12+2=14次；假如27层没碎，在39层碎了，第2个蛋就实验28-38层，最坏情况是11+3=14次；以此类推，无论哪种情况最多14次一定能找到F。
可以看到第1个鸡蛋从14层开始实验，后面的楼层每次增加都少1，这样一来鸡蛋1每多实验一次，就让鸡蛋2少实验一次，也就是说让鸡蛋1实验次数和鸡蛋2的实验次数之和保持在一个平均值，这样无论哪种情况都维持这个值。
这个结果怎么计算来的，假设n表示这个平均值，那么n满足条件$ n+(n-1)+(n-2)+…+1 \geq 100 $，得到$ n \geq 13.65 $，所以n=14。

详细介绍可参考李永乐老师的视频：双蛋问题。
但是这个策略只适用于2个鸡蛋测试的问题，如果有4个或者20个鸡蛋，那最少试多少次可以完成呢？这个时候就该依赖计算机了。

程序

计算机的核心思路就是“暴力”，通过实验每种情况，那么最优的方式自然一目了然。程序不过是在“暴力”的基础上，优化算法，以空间换时间来提高效率求得结果。
用K表示鸡蛋数，N表示楼层数。

方法一：递归

将最终问题转换成小规模问题，函数superEggDrop接收鸡蛋数K和楼层数N，返回最小实验次数。我们并不知道从哪一层开始扔会导致实验次数最少的结果，所以函数枚举1到N层，一层层开始试，返回最小的那个结果。
当从一个楼层i往下扔鸡蛋的时候，只有2种结果，要么鸡蛋碎了，要么没碎。如果碎了，说明F在i以下，同时鸡蛋减少一个，要检测的楼层数变为i-1；如果没碎，说明F在i以上，并且鸡蛋数目没变，楼层数变成了N-i。
这样一来，大问题被拆分成了2个小问题，同时2个小问题变成了同样的问题。
注意要取这2个小问题的答案中大的那个，这样才能保证2个小问题都能实验完成，同时还要加上1，表示本轮实验的1次计数。
K和N的值在每次递归中逐步缩小，递归函数要判断临界情况，当鸡蛋K=1时，只能一层一层试，所以返回值就是楼层数N；当楼层数N=0时，无需测量，直接返回0。
递归过程中存在很多重复的计算，我们用字典将(K,N)和对应的结果缓存起来。
假设楼层最高是10000层，那么最坏1个蛋的情况要试10000次，所以这里采用10000最为边界值。

self.dp=dict()
def superEggDrop(self, K: int, N: int) -> int:
    if K==1:
        return N
    if N==0:
        return 0
    if (K,N) in self.dp:
        return self.dp[(K,N)]
    res=10000
    for i in range(1,N+1):
        res=min(res,max(self.superEggDrop(K-1,i-1),self.superEggDrop(K,N-i))+1)
    self.dp[(K,N)]=res
    return res

时间复杂度，递归函数单次执行是$ O(N) $（单个问题的复杂度：从1到N层楼开始枚举，寻找从哪一层开始扔第1个鸡蛋需要的次数最少），需执行N*K次（问题的个数：相当于算了N层楼K个蛋的所有情况），所以总的时间复杂度 $ O(KN^2) $。

方法二：动态规划

递归采用的是自顶向下的思路，通过“备忘录”的方式缓存了重复计算的结果。而动态规划则采用的是自底向上的思路，从最基本的情况开始推导，直到求得结果。
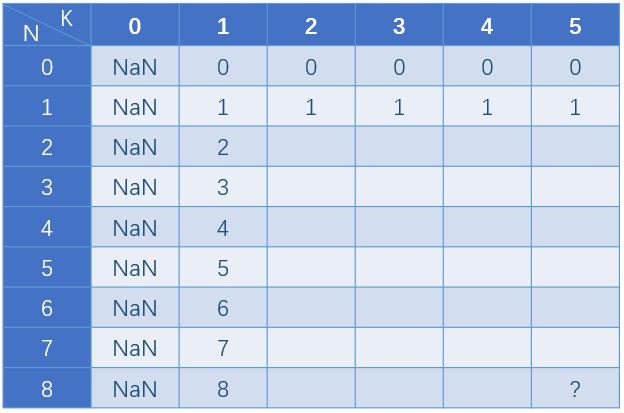
以N=8，K=5为例：

状态初始化

当N=0时，表示没有楼层，无需测试，无论有多少个蛋，测试数量都是0；
当K=0时，表示没有鸡蛋，是无法完成测试的，这里设置为了NaN表示无意义，实际上这里的NaN根本不会参与到后续计算，所以无论你初始化成什么都不影响结果；
当N=1时，表示只有一层，无论多少个鸡蛋，测试一次便可知道结果，碎了F=0，没碎F=1，所以这里全填充为1；
当K=1时，表示只有一个鸡蛋，所以只能一层层测试，测试次数等于楼层数。

构造如下dp表格，dp[i][k]表示i层楼，k个蛋时，最少需要的测试测试，而我们要求的结果就是dp[8][5]。

状态转移

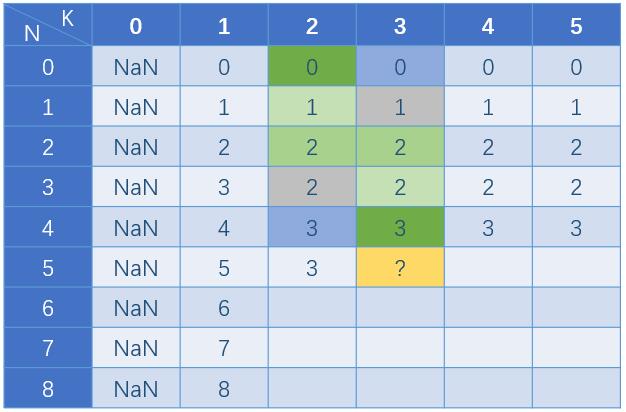
和递归的思路一样，当从第j层扔鸡蛋时，要么鸡蛋碎了，楼层变为j-1，鸡蛋数变为k-1；要么鸡蛋没碎，楼层变为N-j，鸡蛋数不变还是k。但我们并不知道从哪一层开始扔会导致结果最小，所以枚举j一层层去试，状态转移表达式为：

1 2	`for j in range(1, i + 1): dp[i][k] = min(dp[i][k], max(dp[j - 1][k - 1], dp[i - j][k]) + 1)`

i表示当前要求的楼层，k表示当前鸡蛋数。
在表格中的表现形式为图中的金色表示当前要求的dp[5][3],它的值和表格中有背景颜色单元格的值有关，颜色相同的一对取二者中的较大值，例如红色的这对dp[0][2]和dp[4][3]，将较大值加上1，对这5对采取同样的计算，从5个计算结果中取最小的那个，填入dp[5][3]，所以这里应该填3。
以此类推，最终填满整个表格，而最后一个单元格就是问题的答案。

def superEggDrop(self, K: int, N: int) -> int:
    dp=[[0 for _ in range(K+1)] for _ in range(N+1)]
    for k in range(1,K+1):
        dp[1][k]=1
    for i in range(1,N+1):
        dp[i][1]=i
    for i in range(2, N + 1):
        for k in range(2, K + 1):
            dp[i][k]=i  #先初始化为最大次数
            for j in range(1, i + 1):
                dp[i][k] = min(dp[i][k], max(dp[j - 1][k - 1], dp[i - j][k]) + 1)
    return dp[-1][-1]

通过代码显而易见，该程序的时间复杂度仍然是$ O(KN^2) $。

方法三：还是动态规划，但是逆向思维

逆向思维：假如给你K个蛋，你可以测试m次，最多能从多少层楼中找到F？
题目给你的是K个鸡蛋数，N层楼，求最少的m实验次数；现在反过来，有K个鸡蛋，实验m次，最多能从多少层楼中测验出F。
还是用动态规划的思想，但这次状态表示为dp[m][k]=N，即k个蛋，实验m次，一定能在N层中找到F。

状态转移

dp[m][k]=dp[m-1][k-1]+dp[m-1][k]+1
当你从某一层楼扔下一个鸡蛋开始测试的时候，用去1次机会，机会数剩下m-1次，如果鸡蛋碎了，你可以用m-1次和k-1个蛋测试这层楼底下的楼层数；如果没碎，你就可以用m-1次和k个蛋测试这层楼往上的楼层数，再加上这层楼本身算1层，所以你可以从dp[m-1][k-1]+dp[m-1][k]+1这么高的楼层中找到F。

状态初始化

当K=0或者m=0时，即没有鸡蛋或者不扔鸡蛋，都是无法从任何楼层中测出结果的，所以填充0；
m=1，只扔1次鸡蛋，无论你有多少个鸡蛋，都只能在一层楼中测出答案，所以全是1；
K=1，只有1个鸡蛋，最坏结果就是每次扔都不碎，那么就是可以扔多少次，就能在测验多高的楼层。比如m=8，你从第1层开始扔，扔了8次扔到第8层还没碎，如果楼层就是8，那么F=8，但如果有9层，你就不知道F到底是8还是9了，所以扔8次你最多能从8层楼测出F。

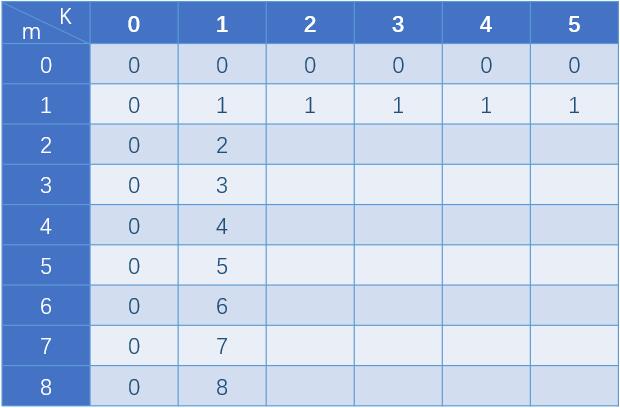
可以对照正向动态规划的初始化表格一起查看，2者实际上是能对应起来的。
这里的原则是不断填充dp表格，当某一个格子大于等于N时，这时的m就是最小实验次数。
dp的行数量仍然可以用N来初始化，m的次数是不会超过N的，因为即便每层都试，最多N次也测试完了。

def superEggDrop(self, K: int, N: int) -> int:
    dp=[[0 for _ in range(K+1)] for _ in range(N+1)]
    for k in range(1,K+1):
        dp[1][k]=1
    for i in range(1,N+1):
        dp[i][1]=i
    for m in range(2, N + 1):
        for k in range(2, K + 1):
            dp[m][k] = dp[m-1][k] + dp[m - 1][k - 1] + 1
            if dp[m][k]>=N:
                return m
    return N

和前面的正向思维不同，这里并没有关注从哪一层开始扔可以得到最小值，减少了对N的枚举，所以时间复杂度降到了$ O(KN) $。

优化

通过状态转移表达式可以看到，要求的dp[m][k]只和dp[m-1][k-1]与dp[m-1][k]2个值有关，也就是说要求的值(图中金色)只和上一行的2个值(图中黄色)相关，所以dp完全可以简化成1维数组，如图所示：

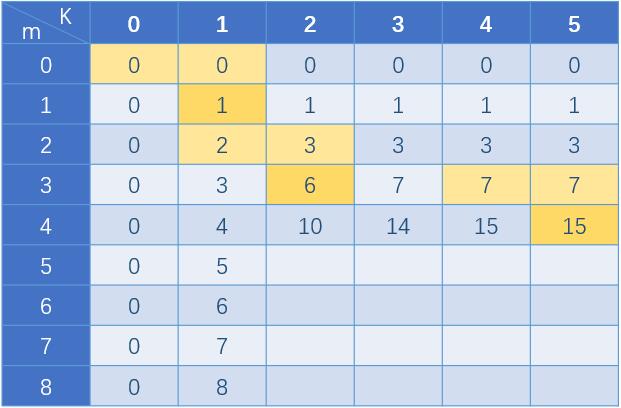
注意这里简化成1维数组需要按列反向求值(从最后一个单元格填充到第一个单元格)，如果正向求值，新值会覆盖旧值，从而会影响后面的计算结果。
同时每一行最末尾的那一格就是当前m行可以到达的最大值，只要这个值能够大于等于N，说明N一定在这一行的区间，所以这一行的m就是要求的结果，空间复杂度可以优化成$ O(K) $。

def superEggDrop(self, K: int, N: int) -> int:
    dp=[0]*(K+1)
    m=0
    while dp[-1]<N:
        for i in range(len(dp)-1,0,-1):
            dp[i]=dp[i]+dp[i-1]+1
        m+=1
    return m