彻底搞懂KMP算法原理

简介

KMP算法是什么？
引用自百度百科：

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度$ O(m+n) $。

也就是说，KMP算法是用来解决字符串匹配问题的，从一个主字符串text中寻找一个子字符串(模式字符串)pattern，看这个子串是否在主串中，比如对于text='abaacababcac'和pattern='ababc'，子串是包含在主串中的，同时它在主串中的索引是5。

字符串匹配暴力法

一般的字符串匹配解法是将2个串的字符进行挨个比较，相当于是把每个字符都比较了一遍，这样是一定能得到结果的，不过显然这样操作导致的时间复杂度是$ O(m*n) $，也就是2个字符串的长度之积，俗称暴力解法。

用图像表示暴力解法的过程如下：
一开始，i和j分别指向主字符串和子字符串，

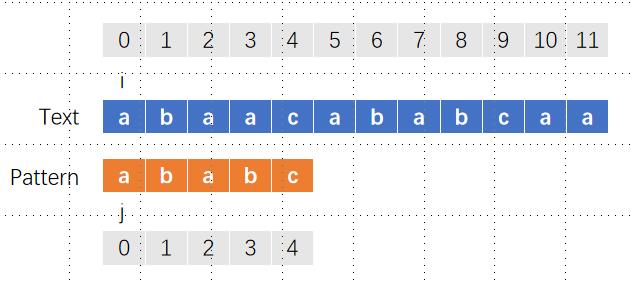
这个时候开始比较t[i]和p[j]，如果匹配则i和j同时向右移动一格，这样i和j同时移动到了位置3，

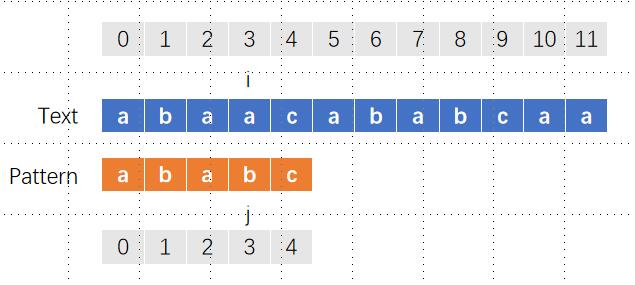
此时i和j不匹配了，需要对i和j进行回退，i回退到了它最开始的下一位置，即位置1，而j回退到位置0

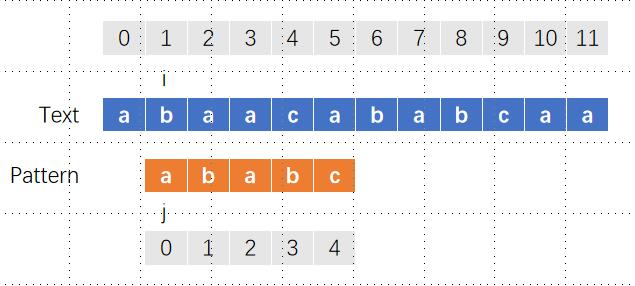
此时i和j仍然不匹配，i继续向右移动一格，即位置2，j依然保持位置0

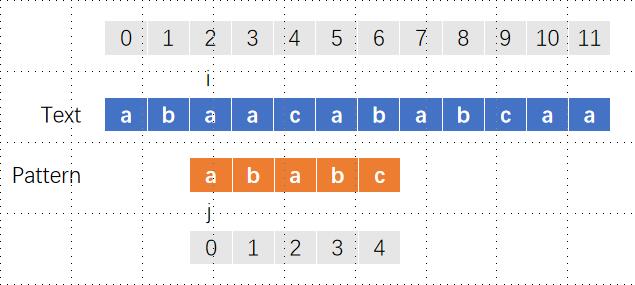
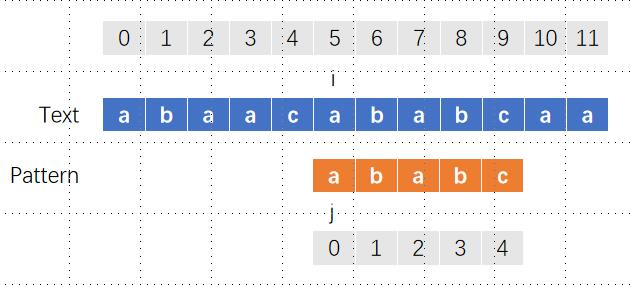
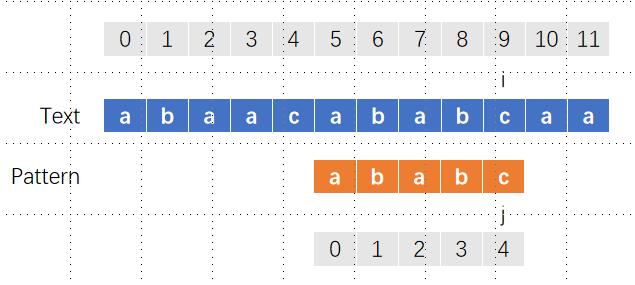
如此反复，每当不匹配时，i都会回到开始匹配的位置同时移动一格，而j回到位置0，当匹配时，i和j同时向右移动，直到j到达子字符串的末尾。

代码表示：

def strStr(self, text: str, pattern: str) -> int:
    n1,n2=len(text),len(pattern)
    if n2==0:
        return 0
    i,j=0,0
    while i<n1:
        if text[i]==pattern[j]:  #相等时同时移动
            i+=1
            j+=1
        else:
            i-=j   #回到最开始匹配的位置
            i+=1   #向右移动一格
            j=0    #j回到位置0
        if j==n2:          #到达字符串末尾，说明匹配成功，返回结果
            return i-n2
    return -1

KMP算法原理

KMP算法则用了一种聪明的办法，当发现字符串不匹配的时候，并不会从头开始比较，因为之前已经匹配成功的字符可以给我们提供一些有用的信息，利用这个信息我们可以将子串移动到某个位置，并从这个位置直接开始比较，它的时间复杂度降到了$ O(m+n) $，也就是2个字符串的长度之和。

网上有很多关于KMP的代码，大体知道是通过计算子串（模式串）自身来获得一个next数组，然后在匹配过程中通过next数组来决定下一个匹配位置，代码虽然不复杂，然而知其然不知其所以然，如果不明白其中原理，那么很难将这个算法写出来。

本文将介绍一种最朴素的KMP算法，目的就在于彻底搞懂KMP算法原理，它的next是怎么来的，以及算法是如何奏效的。

字符串的前缀和后缀

首先我们需要知道字符串的前缀和后缀：
对于字符串ababc来说，它的前缀有[a,ab,aba,abab]，也就是以字符串第一个字符作为开头，同时不包括最后一个字符的所有子串，同理它的后缀有[c,bc,abc,babc]，也就是以字符串最后一个字符作为结尾，同时不包括第一个字符的所有字串。

字符串的最长公共前后缀

了解了这个，我们再来说什么是字符串的最长公共前后缀，说白了，也就是前缀和后缀这2个集合中的相同部分，同时取最长的那个，就是这个字符串的最长公共前后缀。显然，在这个例子中，ababc是没有公共前后缀的。但是对于abab，它的前缀和后缀分别是[a,ab,aba]和[b,ab,bab]，那么它的最长公共前后缀就是ab。

现在，我们的目标就是取得ababc所有子串[a,ab,aba,abab,ababc]的最长公共前后缀的长度，分别保存在next数组中，我们只要知道最大长度即可，并不用关心串具体是什么，而我们目前通过观察即可得出next数组这里是[0,0,1,2,0]，我们先知道这个结果即可，此计算方法后续会说明。

KMP的思路分析

得到这个有什么用，回到刚刚的例子，当我们第一次碰到不匹配时（i和j都等于3的时候）：

此时i和j之前的3个字符aba必然完全匹配的，因为只有前面匹配成功了j才能走到3，而我们又知道aba的最长公共前后缀是a，这可以给我们一个很好的提示，主串中的aba的后缀和字串中的aba前缀有最长的公共部分a，这样一来，我们就没必要重新比较了，直接将相同部分对齐就好了，也就是说让j退回到位置1就可以了，而i保持不变。

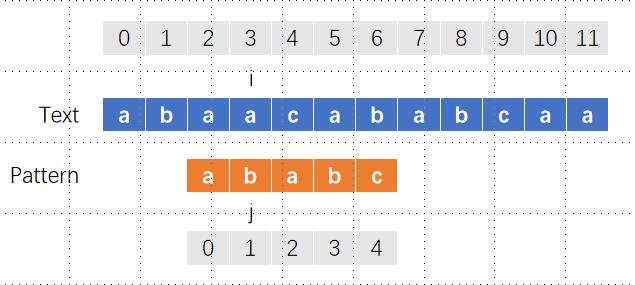
分析一下，为什么j知道应该退回到位置1：

我们知道j是在位置3不匹配的，那么j前面的字符串我们可以知道是aba
前面我们已经得到了next数组，知道aba的最长公共前后缀长度是1
也就是说，我们可以知道i之前1个位置（主串的后缀）和子串开头之后1个位置（子串的前缀）是相同的
进而我们可以让相同部分对齐，也就是让j=next[j-1]

接下来，我们发现i和j仍然不匹配，而j之前的字符a最长公共前后缀是0，此时j退到位置0，i仍然保持不变。

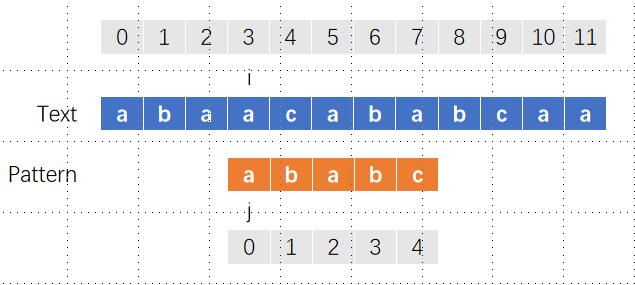
i和j匹配，同时右移一格

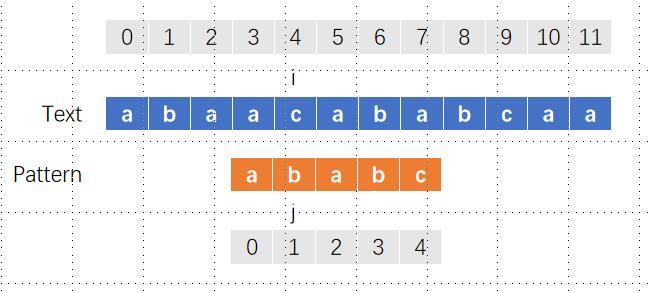
此时i和j不匹配，j=next[j-1]回退到0，然后我们发现i和j仍然不匹配，同时j已经是0了，那么我们就让i往右移动一格。

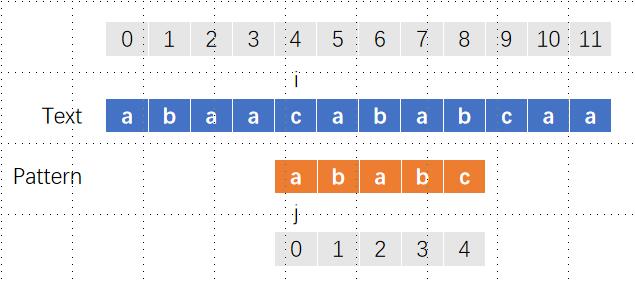
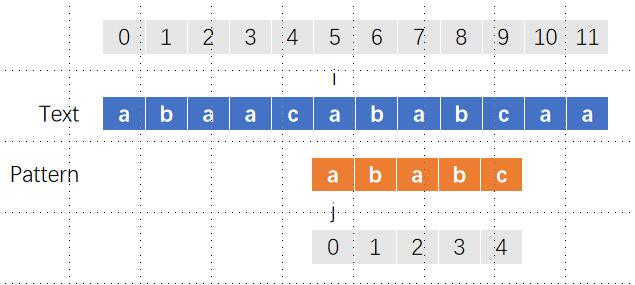
可以看到，相比于暴力解法，i始终在前进，并没有后退（顶多保持不变），然后我们通过next数组来改变j的值。

def strStr(self, text: str, patten: str) -> int:
    next=KMP(patten)       #获取next数组
    n1,n2=len(text),len(patten)
    if n2==0:
        return 0
    i,j=0,0
    while i<n1:
        if text[i]==patten[j]:
            i+=1
            j+=1
        else:
            if j>0:
                j=next[j-1]
            else:
                i+=1
        if j==n2:
            return i-n2
    return -1

求解字符串最长公共前后缀

最后，我们还剩下一个问题，如何求next数组，也就是求模式字符串各个子串的最长公共前后缀长度。
我们先初始化一个和模式字符串长度相等的next数组，在next数组中，第1位默认为0，因为我们规定只有一个字符的字符串没有前缀和后缀，自然公共前后缀长度只能是0。
我们依然设定2个指针i和j，j指向位置0，i从位置1开始依次为next数组进行赋值

我们可以把这个过程依然看作是2个字符串的比较，j指向的是模式字符串的前缀，而i指向的是模式字符串的后缀

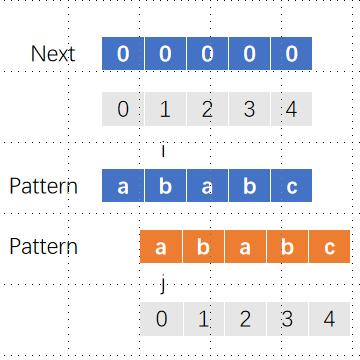
和上面的字符串匹配一样，我们执行同样的处理：

当i和j匹配时，i和j同时右移一格
当i和j不匹配时，如果j不在字符串开头（位置0），就回退到上一个能匹配到的位置
当i和j不匹配时，如果j在字符串开头（位置0），那么i就右移一格

对next[1]赋值：i和j不匹配，同时j已经是字符串开头，赋值0

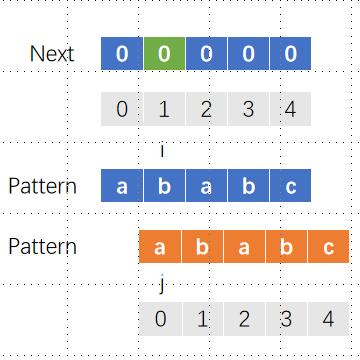
对next[2]赋值，i和j匹配，此时j为0，代表只有1个字符匹配(j+1)，赋值1

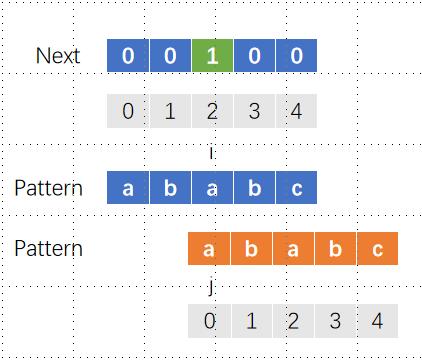
对next[3]赋值，i和j匹配，此时j为1，代表有2个字符匹配(j+1)，赋值2

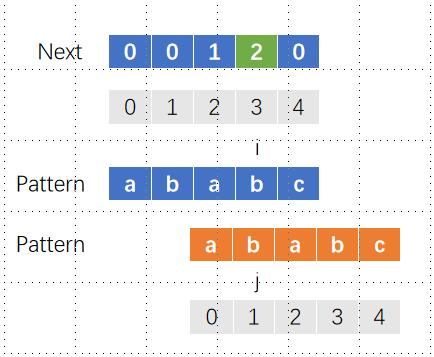
对next[4]赋值，i和j不匹配，此时j为2，可以得知j前面的字符是ab，而ab的最长公共前后缀长度就是next[1]，这个值我们前面已经求得了结果是0，所以j回退到位置0，用代码表示就是j=next[j-1]

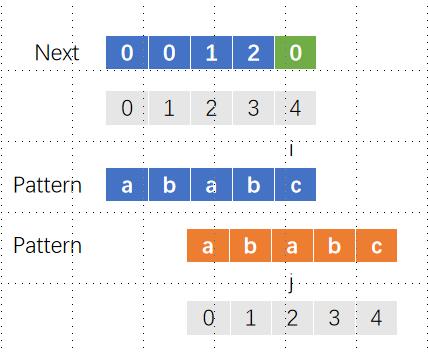
此时i和j仍然不匹配，但是j已为0，无法继续回退，所以直接对next[4]赋值为0

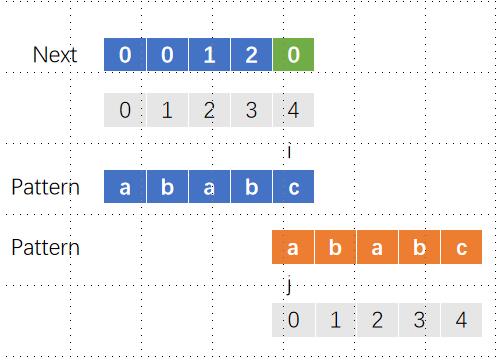
实际上，我们在求解模式字符串ababc的最长公共前后缀长度的时候，不可避免的会对它的子串进行求解，这样可以方便在不匹配时进行回退，这也是动态规划的思想，要求的结果可以用先前已经求得的结果得出。而我们本身就是要对模式字符串的各个子串进行求解，所以可谓一举两得。

def KMP(patten):
    if not patten:
        return []
    n=len(patten)
    next=[0]*n
    i,j=1,0
    while i<n:
        if patten[i]==patten[j]:
            next[i]=j+1
            i+=1
            j+=1
        else:
            if j>0:
                j=next[j-1]
            else:
                next[i]=0
                i+=1
    return next