前言

背包问题实际上是动态规划的一种经典应用，本文想通过介绍一种模板用于解决各种背包问题。

模板统一采用二维数组来表示动态规划的状态，其中行表示物品的价值（或体积、大小、重量等），列表示背包的容量（或目标值）。
行和列都增加了一位，即从1开始计数，一来可以避免边界检查，二来dp[...][target]变得有意义，而非dp[...][target-1]，具体值和数组索引能够对上。根据不同题意来初始化dp，需要注意的是只要涉及到取物品的值，我们需要对索引减1，因为我们是从1开始计数的。

接下来分三种情况考虑动态规划中的状态转移表达式：

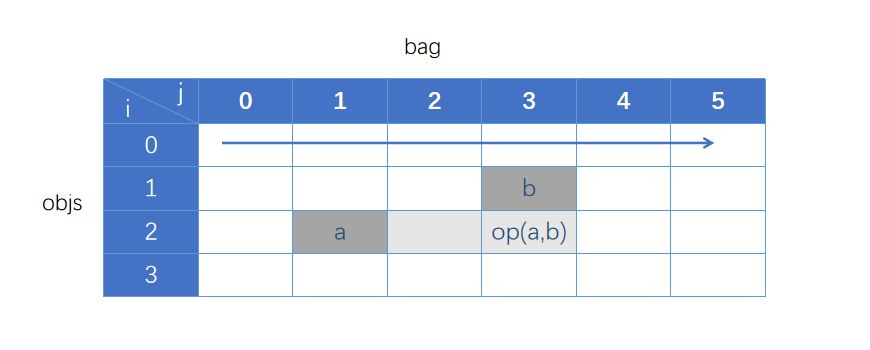
完全背包（每件物品可以无限使用）：dp[i][j]=OPERATE(dp[i-1][j],dp[i][j-objs[i-1]])。这里的OPERATE可以是sum、max、or视具体的问题而定。第二个表达式的索引是i。
完全背包问题状态转移图示

def bag_problem(self, bag: int, objs: List[int]) -> int:
    n=len(objs)+1  #将物品数量增加1，避免边界检查
    #以下两行初始化dp状态
    dp=[[xxx]*(bag+1) for _ in range(n)]
    dp[0][0]=xxx
    for i in range(1,n):
        for j in range(bag+1):
            dp[i][j]=dp[i-1][j]
            if j>=objs[i-1]:  #涉及到物品的索引都需要减1
                dp[i][j]=operate(dp[i-1][j],dp[i][j-objs[i-1]])  #注意第2项是i
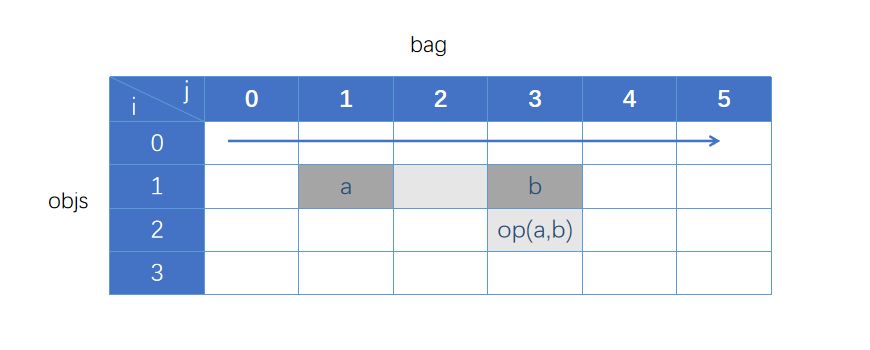
    return dp[-1][-1]

01背包（每件物品只可使用一次）：dp[i][j]=OPERATE(dp[i-1][j],dp[i-1][j-objs[i-1]])，注意和完全背包问题的区别，第二个表达式的索引是i-1。
01背包问题状态转移图示

def bag_problem(self, bag: int, objs: List[int]) -> int:
    n=len(objs)+1  #将物品数量增加1，避免边界检查
    #以下两行初始化dp状态
    dp=[[xxx]*(bag+1) for _ in range(n)]
    dp[0][0]=xxx
    for i in range(1,n):
        for j in range(bag+1):
            dp[i][j]=dp[i-1][j]
            if j>=objs[i-1]:  #涉及到物品的索引都需要减1
                dp[i][j]=operate(dp[i-1][j],dp[i-1][j-objs[i-1]])  #注意第2项是i-1
    return dp[-1][-1]

完全背包排列：dp[i][j]=OPERATE(dp[i-1][j],dp[-1][j-objs[i-1]])，第二个表达式的索引是-1，也即最后一行。

遍历行时的顺序也即访问每件物品的顺序，虽然物品顺序不作限制，但这里有个隐藏条件，遍历过的物品是不会再次访问的，也就是说，选择物品是组合问题，无论先选哪个后选哪个，只要都被选了，只能算作一种状态。
这里归到第3类的问题仍然归属于完全背包范畴，但是它是求排列而非组合，即先拿A或者先拿B，或者拿了A，B之后还可以再次拿A。
在前面的2类问题中，我们优先行或者优先列遍历对结果来说并没有影响，但在这里由于状态转移方程中每次都需最后一行参与计算，所以必须优先列遍历。
完全背包排列问题状态转移图示

def bag_problem(self, bag: int, objs: List[int]) -> int:
    n=len(objs)+1  #将物品数量增加1，避免边界检查
    #以下两行初始化dp状态
    dp=[[xxx]*(bag+1) for _ in range(n)]
    dp[0][0]=xxx  
    for j in range(bag+1):   #内外循环颠倒,按列遍历
        for i in range(1,n):
            dp[i][j]=dp[i-1][j]
            if j>=objs[i-1]:  #涉及到物品的索引都需要减1
                dp[i][j]=operate(dp[i-1][j],dp[-1][j-objs[i-1]]  #第2项是-1，表示最后一行
    return dp[-1][-1]

下面，让我们使用该模板来解决力扣上的各种背包问题。

现在问题的关键就在于把实际问题抽象化为背包问题中的哪一类，然后套用模板即可。
在以下问题中，模板中的二维数组均可优化为一维数组以降低空间复杂度。不用加重记忆负担去考虑什么时候该顺序遍历，什么时候该逆序遍历，以及行列遍历顺序能不能颠倒。当你了解了这个模板的含义，知道动态规划是如何在二维数组上实现的，这些问题都可以迎刃而解。

完全背包

从n种物品中任选，每种物品可以无限取用

方案数

518. 零钱兑换 II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2:

输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。

示例 3:

输入: amount = 10, coins = [10]
输出: 1

问题转换：从n种物品中任选，每种物品可以无限取用，恰好可以装满背包的组合数是多少？

def change(self, amount: int, coins: List[int]) -> int:
    n=len(coins)+1
    dp=[[0]*(amount+1) for _ in range(n)]
    dp[0][0]=1
    for i in range(1,n):
        for j in range(amount+1):
            dp[i][j]+=dp[i-1][j]
            if j>=coins[i-1]:
                # dp[i][j]=sum(dp[i-1][j],dp[i][j-objs[i-1]])
                dp[i][j]+=dp[i][j-coins[i-1]]
    return dp[-1][-1]

特例：求排列非组合

377. 组合总和 Ⅳ

给你一个由不同整数组成的数组nums，和一个目标整数target。请你从nums中找出并返回总和为target的元素组合的个数。
题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

问题转换：和完全背包的恰好装满问题一样，只不过是求排列数而非组合数。

def combinationSum4(self, nums: List[int], target: int) -> int:
    n=len(nums)+1
    dp=[[0]*(target+1) for _ in range(n)]
    dp[0][0]=1
    for j in range(target+1):   #内外循环颠倒,按列遍历
        for i in range(1,n):
            dp[i][j]+=dp[i-1][j]
            if j>=nums[i-1]:
                #这里是-1，不是i-1。dp[i][j]=sum(dp[i-1][j],dp[-1][j-objs[i-1]])
                dp[i][j]+=dp[-1][j-nums[i-1]]
    return dp[-1][-1]

最值

322. 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。
你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

示例 4：

输入：coins = [1], amount = 1
输出：1

示例 5：

输入：coins = [1], amount = 2
输出：2

问题转换：完全背包恰好装满，所需最少物品数。

def coinChange(self, coins: List[int], amount: int) -> int:
    n=len(coins)+1
    dp=[[0]*(amount+1) for _ in range(n)]
    for j in range(1,amount+1):  #初始化为极值
        dp[0][j]=float('inf')
    for i in range(1,n):
        for j in range(amount+1):
            dp[i][j]=dp[i-1][j] #求dp[i-1][j]和dp[i][j-coins[i-1]]+1的较小值，这里是赋值而非累加
            if j>=coins[i-1]:
                # dp[i][j]=min(dp[i-1][j],dp[i][j-objs[i-1]])
                dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1)
    return -1 if dp[-1][-1]==float('inf') else dp[-1][-1]

279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ，返回和为 n 的完全平方数的最少数量。
完全平方数是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

问题转换：完全背包恰好装满，所需最少物品数。把正整数n抽象化为背包容量，从1开始的正整数抽象化为物品，其重量是值的平方。它的平方不能超过n，所以可以确定数字的上限。

def numSquares(self, n: int) -> int:
    m=math.floor(n**0.5)  #最大物品的值
    dp=[[float('inf')]*(n+1) for _ in range(m+1)]
    dp[0][0]=0        
    for i in range(1,m+1):            
        for j in range(n+1):
            dp[i][j]=dp[i-1][j]
            if j>=i**2:
                dp[i][j]=min(dp[i-1][j],dp[i][j-i**2]+1)
    return dp[-1][-1]

注意：python语言采用此方法提交会超出时间限制，一个更好的办法是采用数学来解此题，会用到一个数学定理：四平方和定理。

1449. 数位成本和为目标值的最大数字

给你一个整数数组cost和一个整数target。请你返回满足如下规则可以得到的最大整数：

给当前结果添加一个数位（i + 1）的成本为cost[i]（cost 数组下标从 0 开始）。
总成本必须恰好等于target。
添加的数位中没有数字 0 。

由于答案可能会很大，请你以字符串形式返回。
如果按照上述要求无法得到任何整数，请你返回 “0” 。

示例 1：

输入：cost = [4,3,2,5,6,7,2,5,5], target = 9
输出：”7772”
解释：添加数位 ‘7’ 的成本为 2 ，添加数位 ‘2’ 的成本为 3 。所以 “7772” 的代价为 23+ 31 = 9 。 “977” 也是满足要求的数字，但 “7772” 是较大的数字。
数字成本
1 -> 4
2 -> 3
3 -> 2
4 -> 5
5 -> 6
6 -> 7
7 -> 2
8 -> 5
9 -> 5

问题转换：每个物品体积不一样，完全背包恰好装满，最多可以装多少个物品。数字能选择的越多，必然能得到的数字越大，同时，我们是从1-9开始选择，也就是从数值的小到大，如果确定选择了这个数，也必然是目前最大的，那肯定放在最高位，得到的整数最大。

可完全套用完全背包模板，只需把operate抽象化为一个函数，这个函数类似于max函数，不过更高级，它比较2个值，在能恰好装满背包的前提下，谁组成的数字更大。

def largestNumber(self, cost: List[int], target: int) -> str:
    def maxValue(a,b,v):
        if a is None and b is None:  # 两种方案都不可行，返回None
            return None
        if b is None:    # 其中一种不行，就直接返回另一种
            return a
        b=v+b
        if a is None:
            return b
        n1,n2=len(a),len(b)   # 两种都可以，比较谁的数值更大
        if n1>n2:
            return a
        elif n1<n2:
            return b
        return max(a,b)
    n=len(cost)
    dp=[['']*(target+1) for _ in range(n+1)]  # 标准完全背包模板，只是把operate换成了自定义函数maxValue
    for j in range(1,target+1):
        dp[0][j]=None
    for i in range(1,n+1):
        for j in range(target+1):
            dp[i][j]=dp[i-1][j]
            if j>=cost[i-1]:
                dp[i][j]=maxValue(dp[i-1][j],dp[i][j-cost[i-1]],str(i))
    if dp[-1][-1] is None:
        return "0"
    return dp[-1][-1]

布尔值

139. 单词拆分

给定一个非空字符串 s 和一个包含非空单词的列表wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：

输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。

示例 2：

输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。注意你可以重复使用字典中的单词。

示例 3：

输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

问题转换：完全背包恰好装满，是否存在解决方案，单词用过之后可以再用，所以这里应该采用排列的策略。

def wordBreak(self, s: str, wordDict) -> bool:
    n=len(wordDict)+1
    dp=[[False]*(len(s)+1) for _ in range(n)]
    dp[0][0]=True
    for j in range(len(s)+1):  #内外循环颠倒,按列遍历（单词可以不在乎顺序，和排列类似）
        for i in range(1,n):
            dp[i][j]=dp[i-1][j]
            if j>=len(wordDict[i-1]) and s[j-len(wordDict[i-1]):j]==wordDict[i-1]:
                #这里是-1，不是i-1。
                # dp[i][j]=or(dp[i-1][j],dp[-1][j-objs[i-1]])
                dp[i][j]|=dp[-1][j-len(wordDict[i-1])]
    return dp[-1][-1]

01背包

从n件物品中任选，每件物品只可取用一次

方案数

494. 目标和

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例：

输入：nums: [1, 1, 1, 1, 1], S: 3
输出：5
解释：

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

问题转换：从一堆物品中选出若干个，恰好能装满背包的方案数。

def findTargetSumWays(self, nums: List[int], t: int) -> int:
    s=sum(nums)
    if t>s:
        return 0
    t+=s
    if t%2!=0:
        return 0
    t=t//2     #获取目标值，转换为01背包问题
    n=len(nums)+1
    dp=[[0]*(t+1) for _ in range(n)]
    dp[0][0]=1
    for i in range(1,n):
        for j in range(t+1):
            dp[i][j]+=dp[i-1][j]
            if j>=nums[i-1]:
                # 和完全背包问题不同之处：这里是i-1。
                # dp[i][j]=sum(dp[i-1][j],dp[i-1][j-objs[i-1]])
                dp[i][j]+=dp[i-1][j-nums[i-1]]
    return dp[-1][-1]

最值

474. 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,”0001”,”1”,”0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,”1”} 和 {“10”,”1”,”0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

问题转换：01背包恰好装满，最多可以装多少个物品。注意这里的物品体积可以看作是由0的个数和1的个数2个维度构成的，仍然是01背包问题，只不过将物品的1维变成了2维。

def findMaxForm(self, strs, m: int, n: int) -> int:
    nums = []
    for s in strs:
        num = [0,0]
        for c in s:
            if ord(c) - ord('0') == 0:
                num[0]+=1
            else:
                num[1]+=1
        nums.append(num)
    #转换成01背包问题
    l = len(nums) + 1
    dp = [[[0] * (n + 1) for _ in range(m + 1)] for _ in range(l)]
    for i in range(1,l):
        for a in range(m + 1):
            for b in range(n + 1):
                dp[i][a][b] = dp[i - 1][a][b]
                if a >= nums[i - 1][0] and b >= nums[i - 1][1]:
                    # dp[i][j]=max(dp[i-1][j],dp[i-1][j-objs[i-1]])
                    dp[i][a][b] = max(dp[i][a][b],dp[i - 1][a - nums[i - 1][0]][b - nums[i - 1][1]] + 1)
    return dp[-1][-1][-1]

1049. 最后一块石头的重量 II

有一堆石头，用整数数组stones表示。其中stones[i]表示第i块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为x和y，且x <= y。那么粉碎的可能结果如下：
如果x == y，那么两块石头都会被完全粉碎；
如果x != y，那么重量为 x 的石头将会完全粉碎，而重量为y的石头新重量为y-x。
最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

问题转换：如果把石头分成两组，使两组的重量尽可能相同，那么最终剩下的重量就越小。所以尽可能使2组的石头重量倾向于总重量的一半，问题变成01背包问题：给定一些石头和一个指定容量的背包，最多可以装多少重量的石头（不能超过背包容量）。


def lastStoneWeightII(self, stones: List[int]) -> int:
    n=len(stones)+1
    s=sum(stones)
    t=s//2
    dp=[[0]*(t+1) for _ in range(n)]
    for i in range(1,n):
        for j in range(t+1):
            dp[i][j]=dp[i-1][j]
            if j>=stones[i-1]:
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1])
    return s-2*dp[-1][-1]

布尔值

416. 分割等和子集

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

问题转换：从nums选n个数字能否凑齐s//2。

def canPartition(self, nums: List[int]) -> bool:
    s=sum(nums)
    if s%2!=0:
        return False
    if max(nums)*2>s:
        return False
    s=s//2   #转换成01背包问题
    n=len(nums)+1
    dp=[[False]*(s+1) for _ in range(n)]
    dp[0][0]=True
    for i in range(1,n):
        for j in range(s+1):
            dp[i][j]=dp[i-1][j]
            if j>=nums[i-1]:
                # dp[i][j]=or(dp[i-1][j],dp[i-1][j-objs[i-1]])
                dp[i][j]|=dp[i-1][j-nums[i-1]]
    return dp[-1][-1]

一个模板搞定各种背包问题

前言

完全背包

方案数

特例：求排列非组合

最值

布尔值

01背包

方案数

最值

布尔值