问题

有1000个瓶子里面装满了水，其中1瓶里面被加入了毒药，但是滴入毒药的水在外观上看和普通水是一模一样的，也就是说这1000个瓶子是分不清哪瓶是装有毒药的，除非把装有毒药的水喝进肚子里。现在有一只可怜的猪可以用来实验，将其中一瓶水喂给这只猪喝，如果猪毒发身亡了，说明这瓶水有毒。猪并不需要喝完整瓶水，只需喝到一小口，毒性就会发作，如果水是有毒的话。

由于只有一只猪，所以我们只能一瓶一瓶的去试验，假如毒发的时间是1分钟，那么我们每喂完一瓶水，就等待一分钟，直到猪死亡。值得注意的是，我们只需喂完999瓶水即可，因为如果猪喝完前面的999瓶水还没有中毒的话，说明最后一瓶一定是有毒的，已经不需要再试验了，同时这只猪也是幸运的，它可以告别死亡的命运。所以，我们最多需要花费999分钟，或者说试验999次才能找到这瓶装有毒药的水。

那么问题来了，如果现在不是1只猪，而是有10只猪可以用来试验，那么你最少可以试验几次能找到这瓶有毒的水？

提示：我们可以将水混合到一起喂给猪喝，无论如何，只要猪喝到有毒的水就会死亡。

答案

如果你不熟悉二进制的话，可能会觉得不可思议。不过答案是只需1次，没错，我们只需让每只猪喝1次水，总共花费1分钟即可找到这瓶有毒的水。
猪喝完一瓶水后，它只会有2种状态，要么活着要么死亡，如果把这个状态看作二进制的0和1的话，那么10只猪可以表示$ 2^{10} $个状态，也就是1024个状态，已经超过1000个瓶子了，所以10只猪的前提下，我们只需试验1次即可。

原理

我们先将这1000瓶水，按0-999编号，前面说过10位二进制已经可以表示1024个状态了，所以完全能够表示这其中的所有编号。下面的表格是用二进制表示的所有编号：

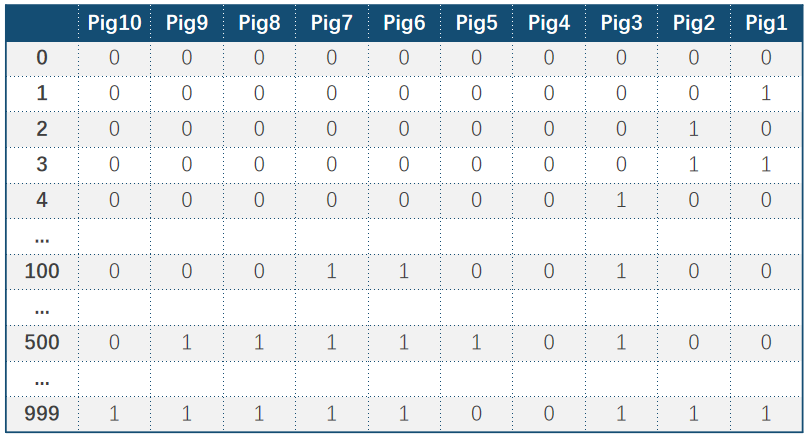
每只猪占据了一个二进制位，比如编号1的猪(Pig1)就相当于二进制的最低位，Pig10为二进制的最高位。
参照这个表格，我们按列给猪喂水，只喂其中标记为1的瓶子。比如Pig1，我们就将瓶子1、瓶子3…瓶子999的水倒出来合到一个桶里，准备喂给猪1，简称桶1。

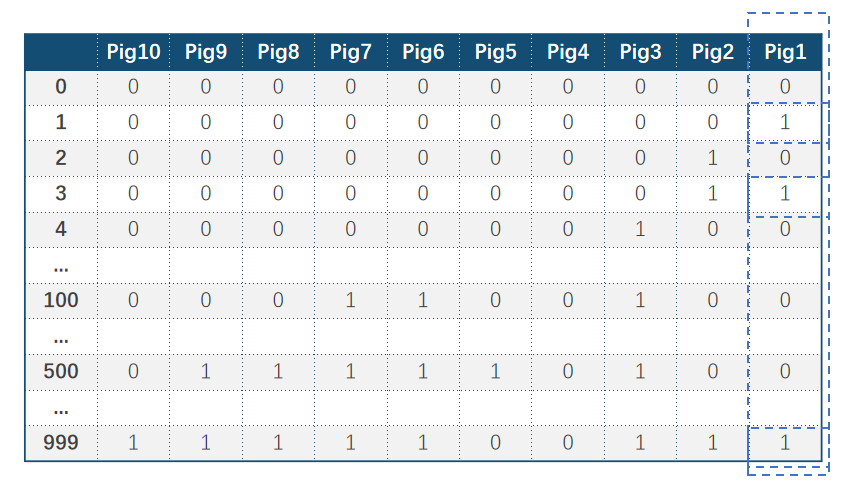
同理，我们将瓶子2、瓶子3…瓶子999的水再倒进另一个桶里准备喂给猪2，简称桶2。

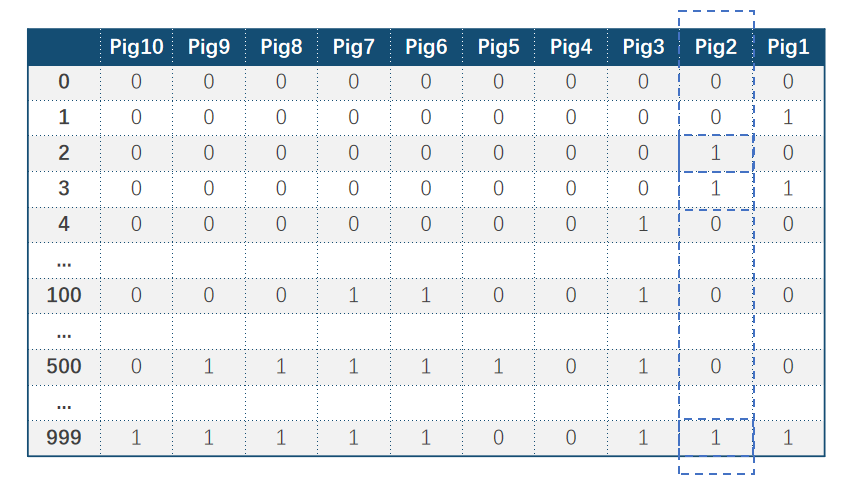
以此类推，我们最终得到了10个桶，然后让10只猪分别喝这10桶水，并记住他们的编号。1分钟后，毒性发作，此时观察这10只猪的状态，根据状态我们就能确定唯一的毒瓶子。
比如只有猪3死亡了，而其他猪都活着，那么一定是4号瓶子是有毒的水，因为除了猪3喝过4号瓶子，其他猪都没有。

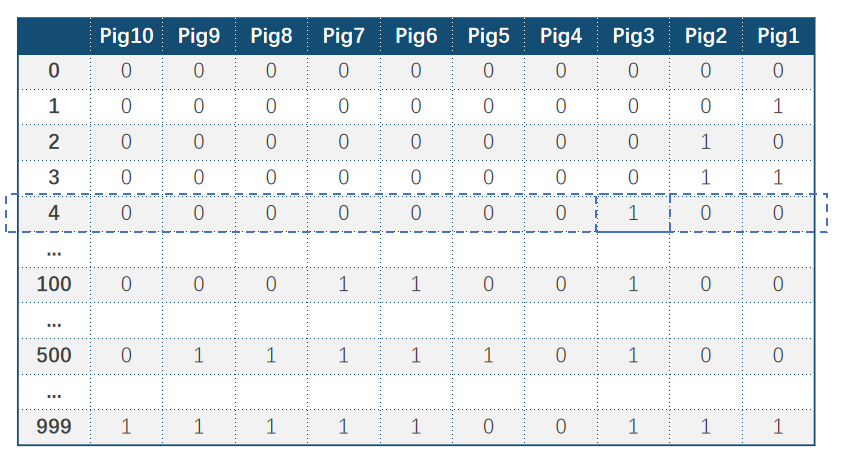
同理，如果只有猪4和猪5活着，其他猪都死了，那么一定是编号999的瓶子，因为死去的猪都要一个共通点，就是它们都喝过999号瓶子的水，而没死的猪一定没喝过999号瓶子。

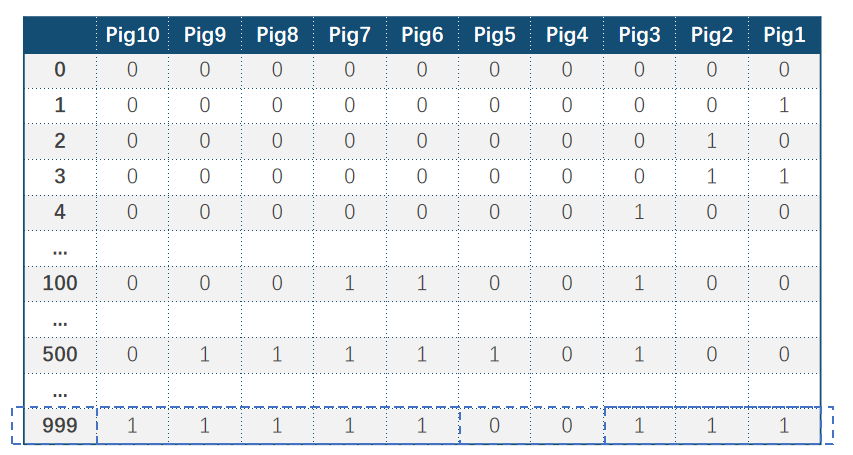
如果够幸运，所有的猪都没有死，那么有毒的水一定在0号瓶子里面，因为只有这瓶水，所有的猪都没有喝过。
所以，根据猪的死亡情况，对照着表格的行，1代表死亡，0代表活着，我们一定能确定一种状态，而这个状态就对应着毒瓶子的编号。

进阶

通过前面的原理分析我们已经知道，在试验1次的情况下，每只猪有2种状态，生或者死，反过来说，如果有2只猪，那么可以最多测试几个瓶子？答案是$ 2^2 =4 $个瓶子，也就是状态数（2）的猪数量（2）次方。
假如我们给4个瓶子编号为0-3，2只猪分别表示A和B，用表格表示：

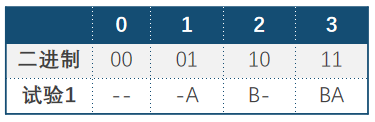
根据表格所示，我们让A喝瓶子1和瓶子3，让B喝瓶子2和瓶子3，一轮结束过后，2只猪的死亡状态可以确定唯一的毒瓶子编号。
为了深刻印象，同理，3只猪可以测试$ 2^3 =8 $个瓶子，我们用ABC代表3只猪，表格表示：

根据表格所示，每只猪对应的喝水情况：

  • A：瓶子1，瓶子3，瓶子5，瓶子7
  • B：瓶子2，瓶子3，瓶子6，瓶子7
  • C：瓶子4，瓶子5，瓶子6，瓶子7

当你按此分配，得到任意一种猪的生死状态后，即使不对照表格，也能通过排除法得到毒瓶子，有兴趣的朋友可以自行验算。

前面都是试验1轮的情况，如果是试验2轮呢？那么每只猪就应该会有3种状态，活着，第1轮死掉、第2轮死掉。以1只猪为例，那么最多可以测试$ 3^1=3 $个瓶子，第1轮喝瓶子1，如果活着进入第2轮喝瓶子2，2轮过后一定能测3个瓶子，由于是3种状态，所以就不能用二进制了，而应该用三进制，表格表示：

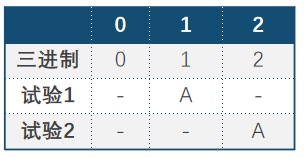
根据表格定义，假如猪最后的状态是状态2，也就是第二轮死掉，那么对应的毒瓶子编号就应该是2。

再来看2只猪试验2次的情况，同理，根据公式应该是$ 3^2 =9$，可以最多测9个瓶子，表格表示为：

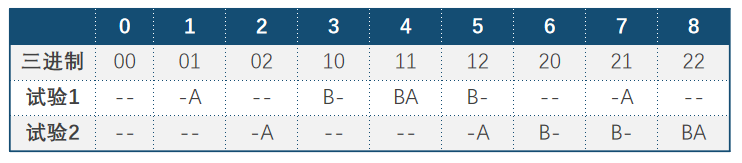
其中，A始终占据数值低位，B始终占据数值高位，试验1中只填充数值为1的位，试验2中只填充数值为2的位，所以喝水策略为:

  • 第一轮：

    • A：瓶子1，瓶子4，瓶子7
    • B：瓶子3，瓶子4，瓶子5

  • 第二轮：

    • A：瓶子2，瓶子5，瓶子8
    • B：瓶子6，瓶子7，瓶子8

以此策略喂猪喝水，我们一定能通过猪最后的状态确定唯一的毒瓶子。

总结：
猪的状态数为试验轮数+1，根据猪的状态数和猪的个数，可以确定最多能测试的瓶子数量，这是一个通用解。

终极

来自力扣的困难题：458. 可怜的小猪
有 1000 只水桶，其中有且只有一桶装的含有毒药，其余装的都是水。它们从外观看起来都一样。如果小猪喝了毒药，它会在 15 分钟内死去。问题来了，如果需要你在一小时内，弄清楚哪只水桶含有毒药，你最少需要多少只猪？
回答这个问题，并为下列的进阶问题编写一个通用算法。

进阶:
假设有 n 只水桶，猪饮水中毒后会在 m 分钟内死亡，你需要多少猪（x）就能在 p 分钟内找出 “有毒” 水桶？这 n 只水桶里有且仅有一只有毒的桶。

提示：
可以允许小猪同时饮用任意数量的桶中的水，并且该过程不需要时间。
小猪喝完水后，必须有 m 分钟的冷却时间。在这段时间里，只允许观察，而不允许继续饮水。
任何给定的桶都可以无限次采样（无限数量的猪）。

解答：
如果你已经看懂了上面的所有分析，那么这题就变成了一道数学题。
猪饮水中毒后会在 m 分钟内死亡，代表一次实验的时间为m分钟，需要在p分钟内找出，则代表可以实验p/m次，也就是是说每只猪可以有p/m+1个状态，而猪的数量是x，瓶子的数量是n，根据公式则有$ (p/m+1)^x=n $，根据题目意思，p，m，n都是已知的，我们的目标就是求得满足该不等式$ (p/m+1)^x>=n $成立的x的最小整数值。
所以，对于这个通用函数，仅仅只需要一行代码：求以(p/m+1)为底，n的对数，并将结果向上取整。

1
2
def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:
    return math.ceil(math.log(buckets)/math.log(minutesToTest//minutesToDie+1))

换一种思路：
猪的状态数代表着n进制，这个n是已知的，这个问题也可以看作是用n进制表示瓶子总数N需要的最小位数。比如对于十进制数字12，在十进制下表示需要2位，而二进制表示下是1100，则需要4位，现在我们只需将瓶子数转换成n进制表示，同时看会占据多少位即可。

1
2
3
4
5
6
7
def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:
    if buckets==1:
        return 0
    def baseN(N, b):
        return "0" if N == 0 else (baseN(N // b, b).lstrip("0") + "0123456789abcdefghijklmnopqrstuvwxyz"[N % b])
    base=minutesToTest//minutesToDie+1
    return len(baseN(buckets-1,base))

我们并不是要通过程序去解一个方程题，重要的是，真正明白其中的原理。