回溯算法的经典应用 - 排列与组合

定义

引用自百度百科：

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

回溯算法实际上是对所有结果的一种暴力枚举方法，以走迷宫为例，它尝试走每条路径，一旦路径不通则退回到最近的分岔点，继续尝试下一条路径，如此反复，直到找到一条正确的路径，或者走完所有路径。对于诸如八皇后、数独这类往往需要枚举所有可能性方案的问题，使用回溯算法再合适不过了。回溯算法采用递归的方式去遍历所有可能结果，时间复杂度高达$ O(n!) $，一般需要伴随“剪枝”操作，以应对庞大的时间复杂度。

假设是走迷宫，这个回溯算法的模板应该是这样：

def backtrace(path,depth,length):
    if depth==length:
        #路径结束（走到头），验证结果
        return
    for node in nodes:
        #枚举所有分岔口可能的节点，加入到路径中
        path.append(node)
        #路径增长，继续下一轮
        backtrace(path,depth+1,length)
        #移除当前节点，准备试下一个
        path.pop(node)

基础题：组合

力扣官方：77.组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

组合是枚举所有的数字，并不涉及到顺序，所以我们只需要从[1-n]挨个选取数字，在之后的回溯中，只选取起始数字往后的数字。我们定义的回溯方法backtrace包含2个参数，参数i表示当前的起始数字，作为可选数字的下限，i之前的数字表示已经选择过，不再重复选择，所以j从i开始遍历；参数arr是一个临时数组，用于存储一个组合的结果，一旦组合中数字的个数达到题目要求的k，表示已确定一个组合，将其归到结果中。这里需注意，数组是一个引用类型，在纳入结果集的过程中，需使用拷贝的新对象res.append(arr[:])，否则你在回溯的过程中会改变原先已纳入结果集的数组，因为操作的是同一个对象。

def combine(self, n: int, k: int) -> List[List[int]]:
    res=[]
    def backtrace(i,arr):
        if len(arr)==k:
            res.append(arr[:])
            return
        for j in range(i,n+1):
            arr.append(j)
            backtrace(j+1,arr)
            arr.pop()
    backtrace(1,[])
    return res

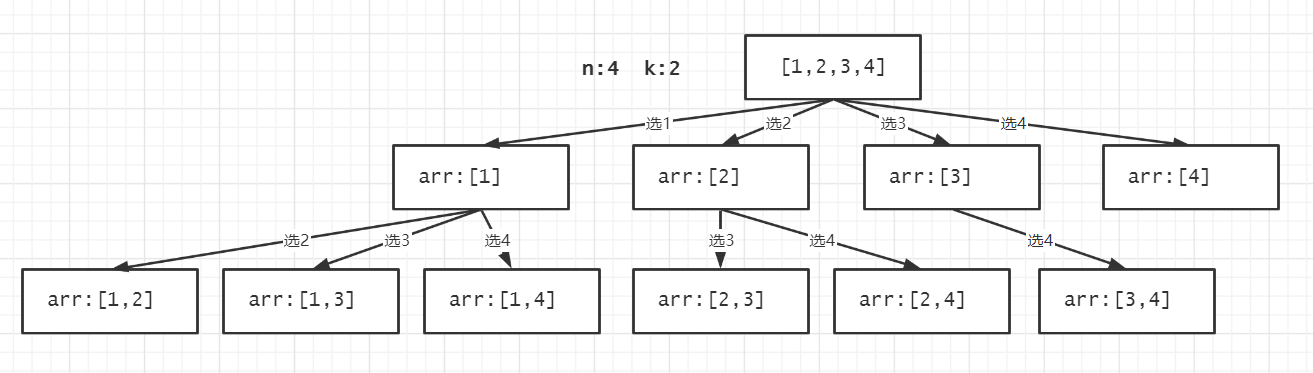
回溯算法可以看作是对一棵树的深度优先遍历（dfs），其中树的每一层节点就对应着代码中的for j in range(i,n+1)循环。

优化：可以注意到，我们是没必要遍历到数字4的，因为到数字4之后就没有数字可选了，是没办法凑齐到题目要求的2个数字的，所以我们可以根据当前组合大小以及需要凑齐的个数k确定可选数字的上限是什么，让可选数字的上界从n变成n-(k-len(arr)-1)。

def combine(self, n: int, k: int) -> List[List[int]]:
    res=[]
    def backtrace(i,arr):
        if len(arr)==k:
            res.append(arr[:])
            return
        for j in range(i,n+1-(k-len(arr)-1)):  #剪枝
            arr.append(j)
            backtrace(j+1,arr)
            arr.pop()
    backtrace(1,[])
    return res

这里以从4个数字选取3个为例，你可以看到加上这个条件之后达到的剪枝效果，避免了无意义的枚举。红色的箭头表示我们剪掉的位置，不会再进行后续的遍历。

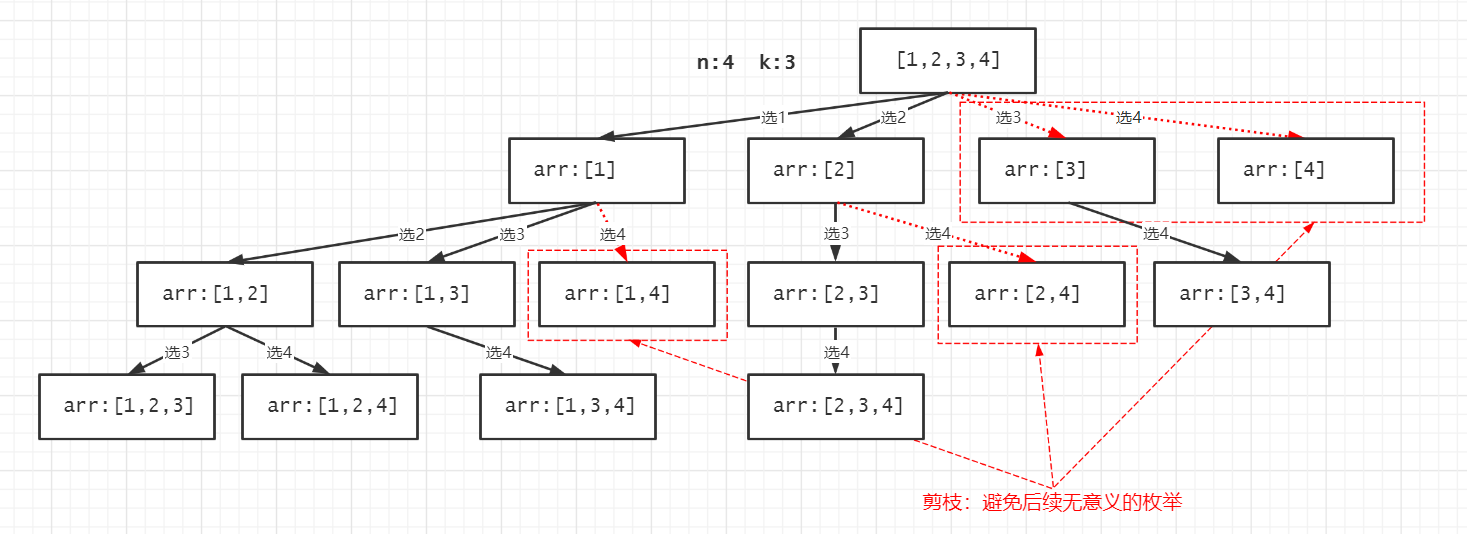
基础题：排列

无重复数的排列

力扣官方：46.全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

排列与组合的不同之处在于，排列不仅要选择出数字，而且还需要关注数字的所在顺序，而组合是不关注排列顺序的。比如对于[1,2,3]和[3,2,1]来说，这2者算作同一个组合，因为它们都具备同样的3个数字1,2,3，而这2者不能算作同一个排列，因为3个数字的顺序不一样。

在排列中，不可从起始数字开始枚举，或者说排列是没有起始数字的，每次必须从头开始遍历for j in range(n)，因为排在后面的数字可能被取到前面，而在组合中，由于不在乎顺序，所以我们从前往后取即可。排列不一样，每个数字都有可能被第一次选到（处于位置0），所以在排列中，我们必须额外记录数字是否被取用，你可以直接在arr中判断是否存在某数，但这将耗费$ O(n) $的时间复杂度（遍历整个数组），常规办法是采用空间换时间的方式，用一个used数组记录数字是否被选用，它存储的状态和arr中的元素保持一致，当arr发生改变时，同步维护used的状态。当数字存在arr中时，used标记该数字为true，反之，标记该数字为false。

由于是对序列进行全排列，我们统一用索引来代替具体的数字。

def permute(self, nums: List[int]) -> List[List[int]]:
    n=len(nums)
    res=[]
    used=[False]*n
    def backtrace(i,arr):
        if i==n:
            res.append(arr[:])
            return
        for j in range(n):
            if used[j]:
                continue
            used[j]=True
            arr.append(nums[j])
            backtrace(i+1,arr)
            arr.pop()
            used[j]=False
    backtrace(0,[])
    return res

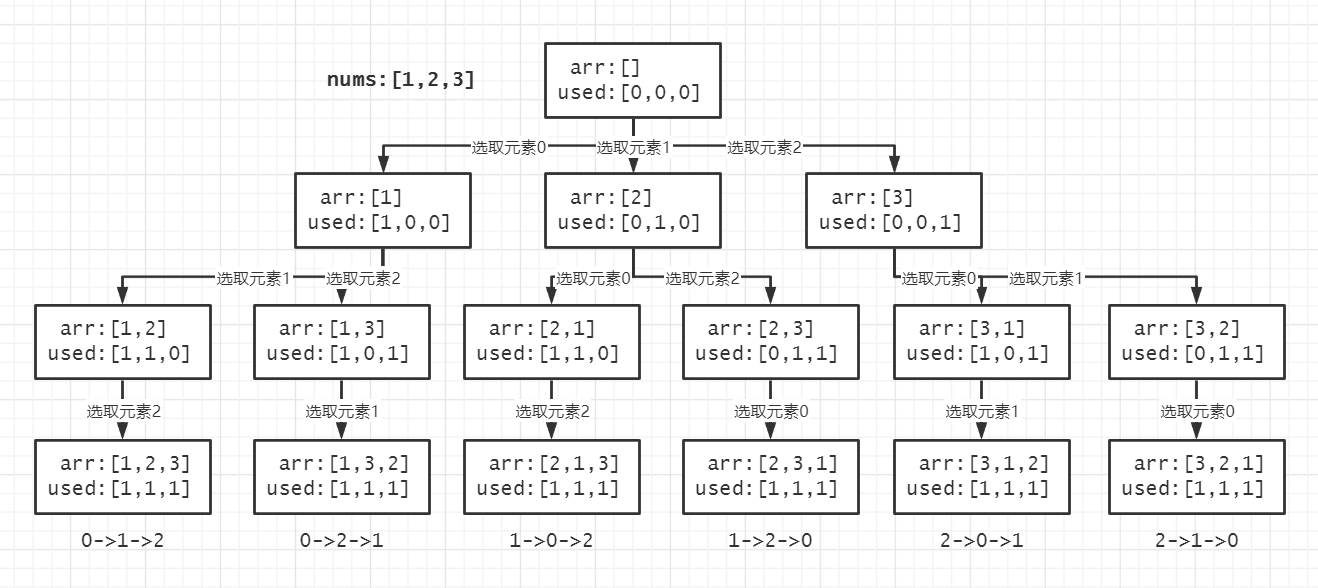
有重复数的排列

力扣官方：47.全排列II

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

该题与上一题不同之处是序列中包含了重复的数字，而重复的数字得到的排列应该去重。比如对于无重复数序列[1,2,3]，可以得到的排列个数为3*2*1=6，而有重复数序列[1,1,2]得到的6个排列中，会得到2个[1,1,2]（第1个1和第2个1位置不同的排列），这里面只能保留一个结果。

为了满足这一条件，我们在回溯过程中就进行剪枝操作，为了更容易比较重复数，第1步先对数组进行排序，这样重复数全部排在了一起；第2步除了判断当前数是否使用if used[j]剪枝外，继续对重复数进行剪枝if j>0 and nums[j]==nums[j-1] and not used[j-1]，如果前一个重复的数字还没用过，则优先前面的排列，该分支被剪掉。

def permuteUnique(self, nums: List[int]) -> List[List[int]]:
    nums.sort()      #将序列排序
    n=len(nums)
    res=[]
    used=[False]*n
    def backtrace(i,arr):
        if i==n:
            res.append(arr[:])
            return
        for j in range(n):
            if used[j]:
                continue
            if j>0 and nums[j]==nums[j-1] and not used[j-1]:  #剪枝：前一个重复的数字还没用过
                continue
            used[j]=True
            arr.append(nums[j])
            backtrace(i+1,arr)
            arr.pop()
            used[j]=False
    backtrace(0,[])
    return res

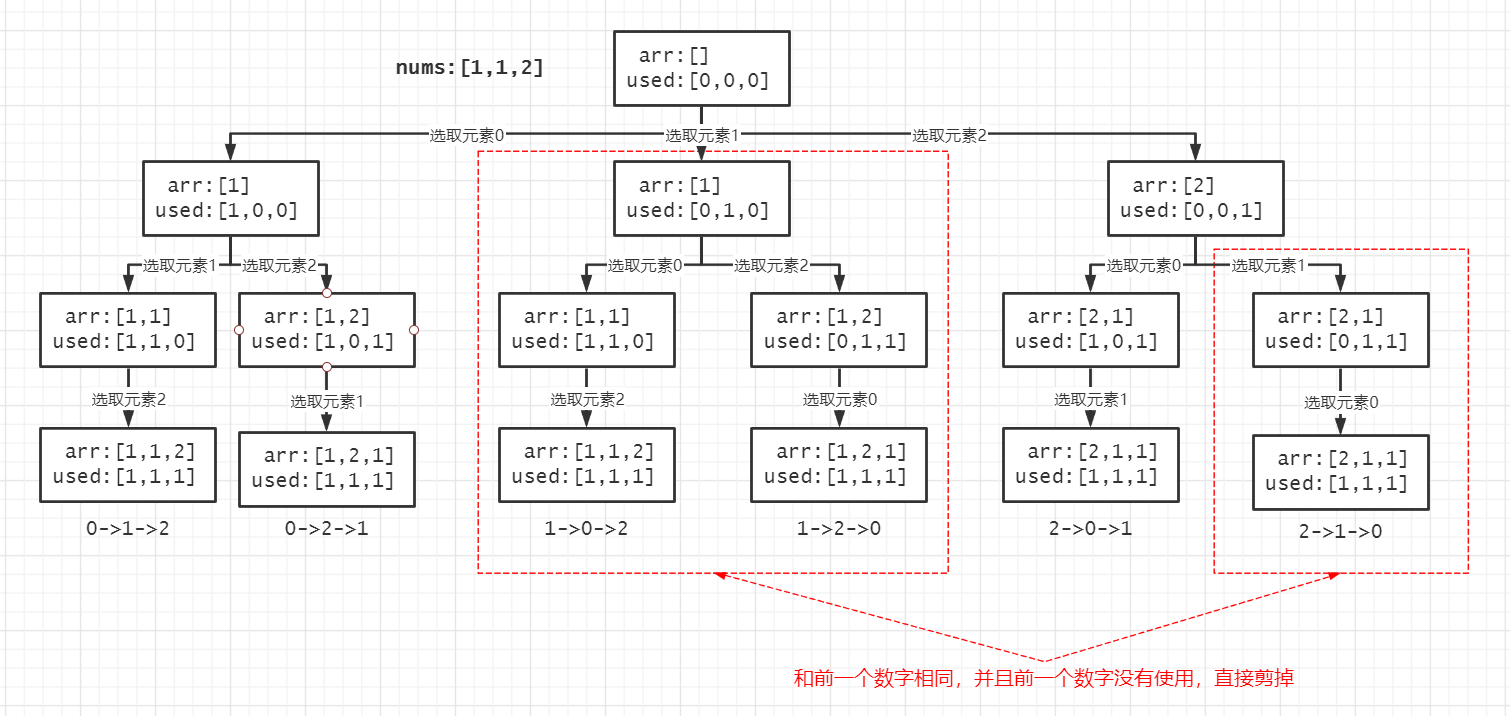
应用题：组合总和

无重复数任意长度组合总和

力扣官方：39.组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
[2,2,2,2],
[2,3,3],
[3,5]
]

此题和之前的基础题组合，有2个区别：

基础题组合的回溯退出条件是组合数量达到目标值，该题的回溯退出条件是组合总和等于目标值；
组合中的数字可以无限重复选用

所以我们这里相比于普通组合，需要做以下改动，回溯函数增加t参数，用于记录当前已累加的总和，回溯函数的返回改为判断是否超出目标值，当大于或者等于目标值后不再进行回溯（后续和只会增大，不会再产生满足要求的结果），如果等于目标值则我们找到一个答案；由于数字可以重复选用，所以相比于普通组合的backtrace(j+1,arr)，进入回溯仍然从j开始，backtrace(j,arr,t+candidates[j])。

def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
    res=[]
    n=len(candidates)
    def backtrace(i,arr,t):
        if t>=target:
            if t==target:
                res.append(arr[:])
            return
        for j in range(i,n):
            arr.append(candidates[j])
            backtrace(j,arr,t+candidates[j])  #继续从j开始回溯
            arr.pop()
    backtrace(0,[],0)
    return res

以candidates = [2,3,5], target = 8为例，以下就是回溯路径，当组合总和大于等于目标值8时回溯返回，标蓝的叶子节点表示总和正好等于目标值，标红的叶子节点表示总和超过目标值。

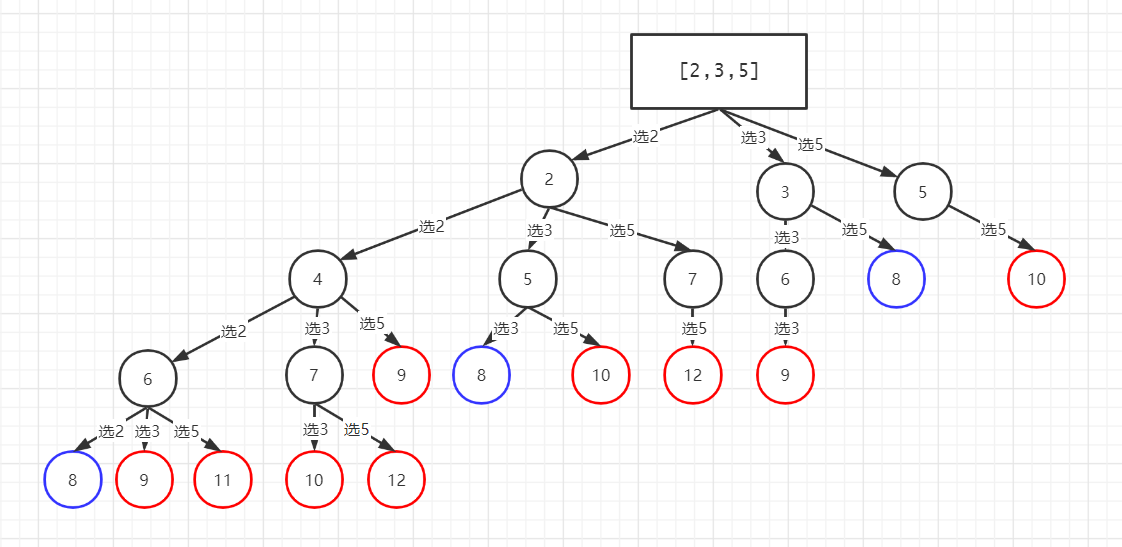
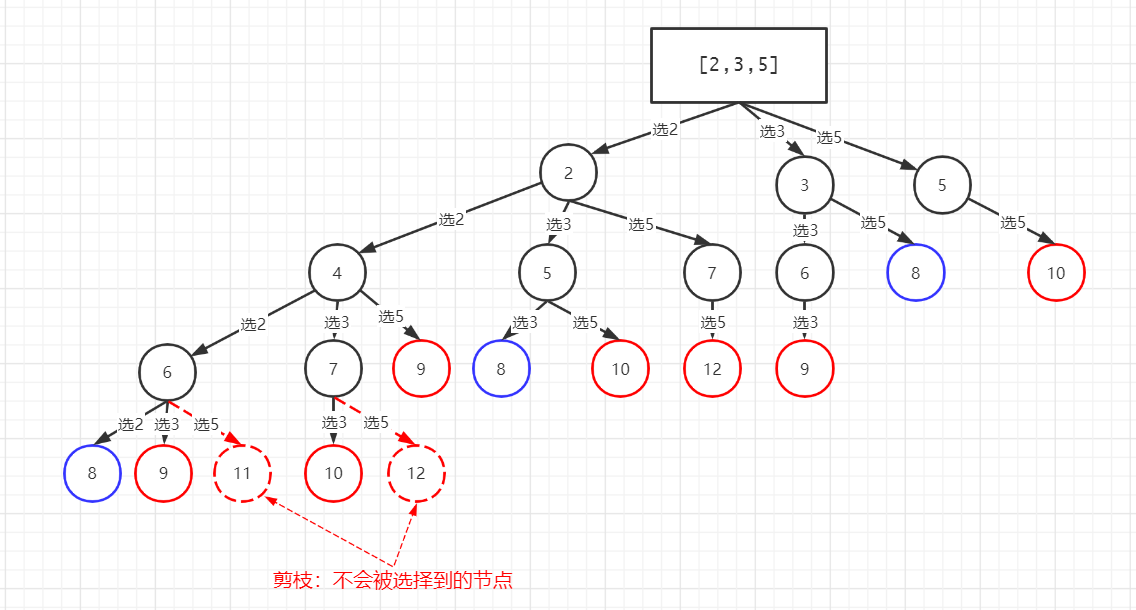
优化：不难发现，在回溯的for循环中，如果当前节点已经超过了目标值，后续的循环都是没有必要的，因为总和一定会比当前的还大，不过这个需要一个前提就是序列是按升序排列的。我们可以先花费$ nlog(n) $的时间复杂度对序列排序，进而就可以在此基础上进行剪枝操作。

def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
    res=[]
    n=len(candidates)
    candidates.sort()         #排序
    def backtrace(i,arr,t):
        if t==target:
            res.append(arr[:])
            return
        for j in range(i,n):
            if t+candidates[j]>target:   #剪枝
                break
            arr.append(candidates[j])
            backtrace(j,arr,t+candidates[j])
            arr.pop()
    backtrace(0,[],0)
    return res

可以看到，我们把判断大于目标值的逻辑移到了for循环中，一旦出现大于目标值则直接退出循环，后续的节点不会再次进入回溯，实现剪枝效果。所谓剪枝，就是减少回溯的路径，图像表示为从树中剪去枝干。

有重复数任意长度组合总和

力扣官方：40.组合总和II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]

此题与上一题的区别是，数组中包含重复的元素，同时每个数组中的元素只能选择一次，只能选择一次这个条件在代码中体现为backtrace(j+1,arr,t+candidates[j])，即从下一个位置开始回溯。由于存在重复的元素，为了避免产生重复的组合，我们可以采用前面讲无重复排列时相同的办法：先对数组进行排序，之后根据当前数字和前一个数字是否相同判断是否重复组合。由于数组已经排序，我们可以继续使用上一题的剪枝方法。

def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
    res=[]
    n=len(candidates)
    candidates.sort()
    def backtrace(i,arr,t):
        if t==target:
            res.append(arr[:])
        for j in range(i,n):
            if t+candidates[j]>target:  #剪枝：去除无意义的路径
                break
            if j>i and candidates[j]==candidates[j-1]:  #剪枝：去除重复的组合
                continue
            arr.append(candidates[j])
            backtrace(j+1,arr,t+candidates[j])
            arr.pop()
    backtrace(0,[],0)
    return res

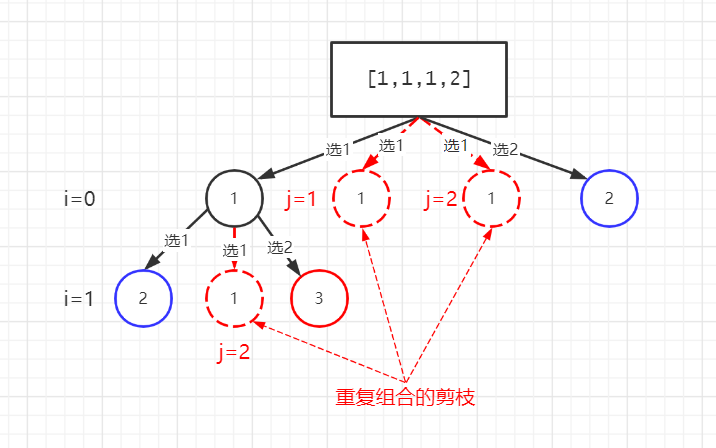
以candidates = [1,1,2], target = 2为例，我们最终只会得到[1,1]和[2]二种结果。

无重复数指定长度组合总和

力扣官方：216.组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

该题可以看作是在数组[1,2,3,4,5,6,7,8,9]中选择k个数，其和要等于n，根据题目意思我们可以得到3个信息：

数组是有序的（可以剪枝）
每种组合中不存在重复的数字（每个数字只能使用一次，回溯要从下一个数字开始backtrace(j+1,...)）
数组中的每个数字都不重复（对于解集不能包含重复组合的约束，我们无须进行排重剪枝）

def combinationSum3(self, k: int, n: int) -> List[List[int]]:
    res=[]
    def backtrace(i,arr,t):
        if len(arr)==k:
            if t==n:
                res.append(arr[:])
            return
        for j in range(i,10):
            if j+t>n:   #剪枝
                break
            arr.append(j)
            backtrace(j+1,arr,t+j)
            arr.pop()
    backtrace(1,[],0)
    return res

总结

对于有重复数的排列或者组合，我们需要先对数组进行排序，让相同的数排在一起，进而方便排重
排列涉及到顺序，每个位置都可以是所有数字，所以每次从头开始选取数字for j in range(n)；组合不涉及顺序，所以我们依次选择，选取时会从起始位置开始for j in range(i,n)
对于数字是否可以重复选用，决定回溯时是从当前位置或是下一个位置：backtrace(j,...)或backtrace(j+1,...)
对于求组合总和问题（每个数字都是正整数，和越加越大），可以先将数组排序，然后进行剪枝优化